Расчет простейших пространственных ферм.
Усилия в простейших фермах легко определяются по способу вырезания узла последовательным разложением силы на три направления. Пусть, например, требуется определить усилия S1 и S2=S3 в стержнях простейшей трехстержневой фермы по рис. 7.4 при действии на узел О вертикальной силы Р.
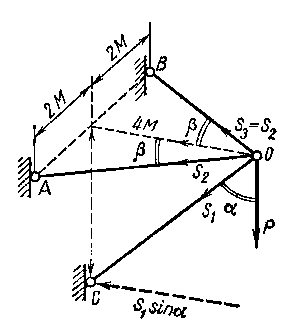
Рисунок 1.8.4
Проектируя все силы, действующие на узел О, на вертикальную ось, перпендикулярную плоскости стержней S2 и S3 получаем:
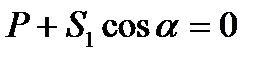
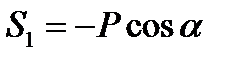
Проектируя силы, действующие на узел О, на горизонталь и вводя равнодействующую сил S2 и S3 которую обозначим R23 получаем
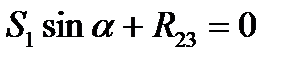
откуда
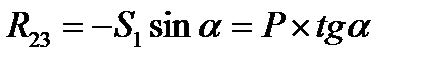
По равнодействующей сил S2 = S3, принимая во внимание, что S2=S3 находим составляющую
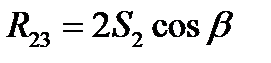
откуда
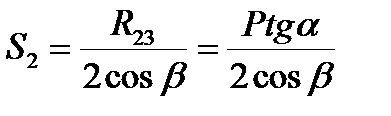
Нередко расчет пространственных, призматических ферм можно осуществлять путем разложения их на отдельные плоские фермы, причем нагрузка произвольного направления разлагается при этом на составляющие, действующие в плоскостях отдельных плоских ферм.
Рассмотрим, например, пространственную сетчатую ферму, представленную на рис. 1.8.5.
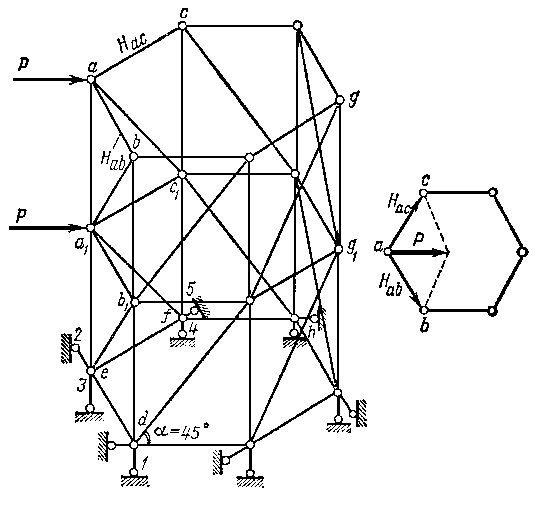
Рисунок 1.8.5
Решетка дается лишь в вертикальных гранях этой пространственной фермы, никаких поперечных связей не требуется. Нетрудно убедиться в неизменяемости данной фермы, применяя метод нулевой нагрузки. Определим усилия в стержнях этой фермы, если на нее действуют горизонтальные силы по диагонали шестиугольного поперечного сечения фермы (аg, а1g1 ) Каждую из сил разлагаем на две горизонтальные составляющие, например силу Р на Нac Нab расположенные в плоскостях граней фермы асfe и аbdе (рис. 1.8.6).
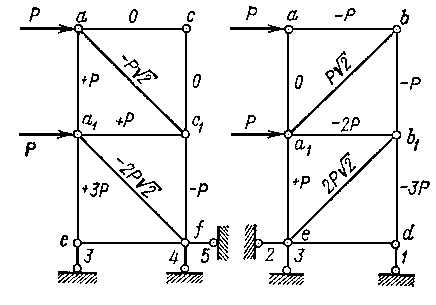
Рисунок 1.8.6.
Внешние силы теперь действуют в плоскостях граней асfe и аbdе. Следовательно, усилия возникают только в элементах этих плоских ферм. Очевидно,
Нас = Нab = Ha1b1= Р.
Рассматривая теперь плоские фермы асfe и аbdе отдельно, определяем усилия в их элементах. Значения этих усилий указаны рис. 1.8.6. Суммарные усилия стержней аа1, а1е и 3 пространственной фермы будут
Saa1=P Sa1e=4P S3=-6P
Дата добавления: 2016-01-18; просмотров: 1000;
