Алгоритм обработки результатов и расчета показателей надежности

2.2.1. Формирование статистического ряда

При большом числе испытываемых объектов полученный массив наработок {…, t_i, …} является громоздкой и мало наглядной формой записи случайной величины T. Поэтому для компактности и наглядности выборка представляется в графическом изображении статистического ряда – гистограмме наработки до отказа. Для этого необходимо:

- установить интервал наработки [t_min, t_max] и его длину 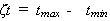, где

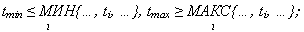
- разбить интервал наработки [t_min, t_max] на k интервалов равной ширины 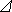t – шаг гистограммы

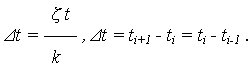
- подсчитать частоты появления отказов во всех k интервалах

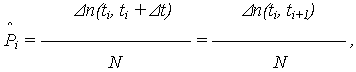
где 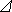n(t_i, t_i + 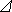t) – число объектов, отказавших в интервале [t_i, t_i + 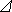t].

Очевидно, что

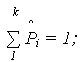
- полученный статистический ряд представляется в виде гистограммы, которая строится следующим образом. По оси абсцисс (t) откладываются интервалы 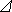t, на каждом из которых, как на основании, строится прямоугольник, высота которого пропорциональна (в выбранном масштабе) соответствующей частоте 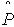. Возможный вид гистограммы приведен на рис. 2.

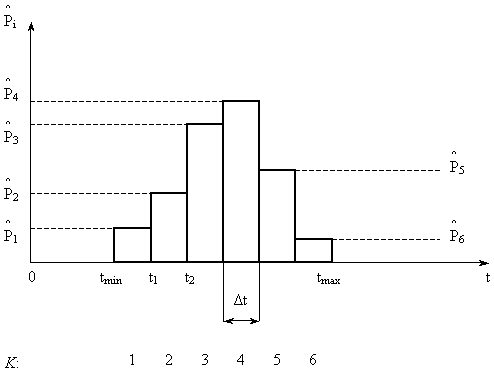
Рис. 2

2.2.2. Расчет эмпирических функций

Используя данные сформированного статистического ряда, определяются статистические оценки показателей надежности, т. е. эмпирические функции:

- функция распределения отказов (оценка ВО)

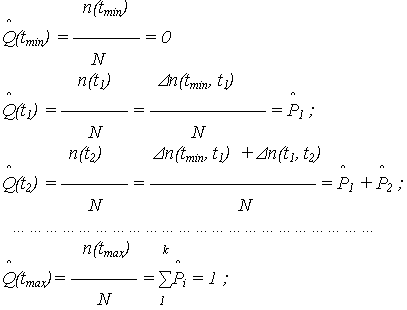
- функция надежности (оценка ВБР)

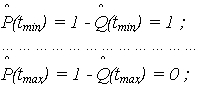
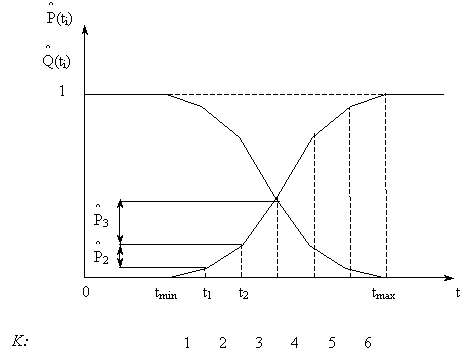
Рис. 3

- плотность распределения отказов (оценка ПРО)

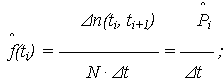
- интенсивность отказов (оценка ИО)

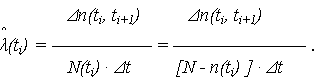
Рис. 4

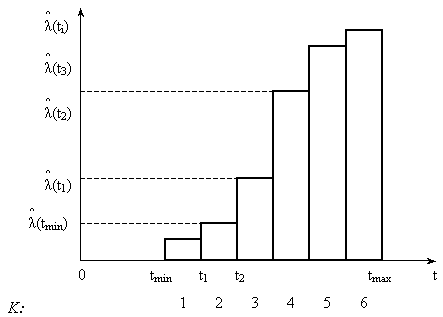
Рис. 5

На рис. 3, 4, 5 приведены соответственно графики статистических оценок 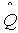(t),

Правила построения графиков ясны из приведенных выше расчетных формул. Каждый из графиков имеет свой масштаб.

2.2.3. Расчет статистических оценок числовых характеристик

Для расчета статистических оценок числовых характеристик можно воспользоваться данными сформированного статистического ряда.

Оценки характеристик определяются:

- оценка средней наработки до отказа (статистическое среднее наработки):

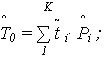
- оценка дисперсии наработки до отказа (эмпирическая дисперсия наработки):

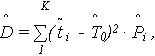
где 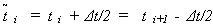– середина i-го интервала наработки, т. е. среднее значение наработки в интервале.

Оценка СКО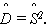

Целесообразно рассчитать оценки и некоторых вспомогательных характеристик рассеивания случайной величины T:

- выборочный коэффициент асимметрии наработки до отказа

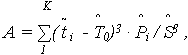
- выборочный эксцесс наработки до отказа

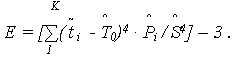
Эти характеристики используются для выбора аппроксимирующей функции.

Так коэффициент асимметрии является характеристикой «скошенности» распределения,

например, если распределение симметрично относительно МО, то A = 0.

На рис. 6, а распределение f₂(t) имеет положительную асимметрию A > 0, а f₃(t) – отрицательную A < 0.

Эксцесс характеризует «крутость» (остро- или плосковершинность) распределения.

Для нормального распределения E = 0.

Кривые f(t), более островершинные по сравнению с нормальной, имеют E > 0, а наоборот – более плосковершинные, E < 0 (рис.6, б).

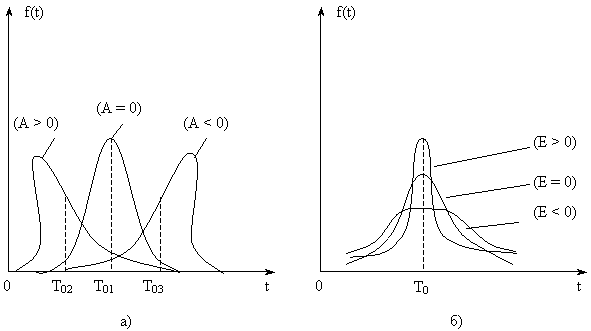
Рис. 6

2.2.4. Выбор закона распределения

Выбор закона распределения состоит в подборе аналитической функции наилучшим образом аппроксимирующей эмпирические функции надежности.

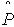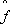Выбор, в значительной мере, процедура неопределенная и во многом субъективная, при этом многое зависит от априорных знаний об объекте и его свойствах, условиях работы, а также анализа вида графиков (t), 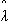(t), (t).

Очевидно, что выбор распределения будет зависеть, прежде всего, от вида эмпирической функции ПРО 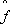(t), а также от вида - 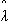(t). Так коэффициентИтак, выбор закона распределения носит характер принятия той или иной гипотезы.

Предположим, что по тем или иным соображениям, выбран гипотетический закон распределения, заданный теоретической ПРО

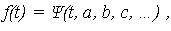
где a, b, c, … - неизвестные параметры распределения.

Требуется подобрать эти параметры так, чтобы функция f(t) наилучшим образом сглаживала ступенчатый график 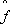(t). При этом используется следующий прием: параметры a, b, c, … выбираются с таким расчетом, чтобы несколько важнейших числовых характеристик теоретического распределения были равны соответствующим статистическим оценкам.

На графике вместе с 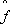(t) строится теоретическая ПРО f(t), что позволяет визуально оценить результаты аппроксимации (расхождения между 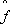(t) и f(t). Поскольку эти расхождения неизбежны, то возникает вопрос: объясняются ли они случайными обстоятельствами, связанными с тем, что теоретическое распределение выбрано ошибочным? Ответ на этот вопрос дает расчет критерия согласия.

2.2.5. Расчет критерия согласия

Критерий согласия – это критерий проверки гипотезы о том, что случайная величина T, представленная своей выборкой, имеет распределение предполагаемого типа.

Проверка состоит в следующем. Рассчитывается критерий, как некоторая мера расхождения теоретического и эмпирического распределений, причем эта мера является случайной величиной.

Чем больше мера расхождения, тем хуже согласованность эмпирического распределения с теоретическим, т. е. меньше мала, то гипотезу о выборе закона распределения следует отвергнуть, как мало правдоподобную.

В противном случае – экспериментальные данные не противоречат принятому распределению.

Из известных критериев наиболее применяемый критерий согласия 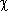² (хи-квадрат) Пирсона.

Проверка согласованности распределений по критерию 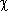² производится следующим образом:

- рассчитывается критерий 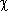² (мера расхождения)

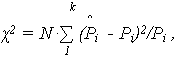
где 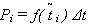– теоретическая частота (вероятность) попадания случайной величины в интервал [t_i, t_i + 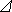t];

- определяется число степеней свободы R = k – L ,

где L – число независимых условий, наложенных на частоты 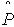_i , например:

а) условие ;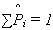

б) условие совпадения ;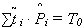

в) условие совпадения 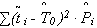= D и т. д.

Чаще всего L = 3. Чем больше число степеней свободы, тем больше случайная величина 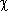² подчиняется распределению Пирсона;

- по рассчитанным 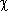² и R определяется вероятность P того, что величина, имеющая распределение Пирсона с R степенями свободы, превзойдет рассчитанное значение 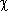².

Ответ на вопрос: насколько мала должна быть вероятность P, чтобы отбросить гипотезу о выборе того или иного закона распределения – во многом неопределенный.

На практике, если P < 0,1, то рекомендуется подыскать другой закон распределения.

В целом, с помощью критерия согласия, можно опровергнуть выбранную гипотезу, если же P достаточно велика, то это не может служить доказательством правильности гипотезы, а указывает лишь на то, что гипотеза не противоречит данным эксперимента.

Контрольные вопросы:

1. Что представляет математическая модель, и для каких целей она используется в задачах надежности?

2. Из каких условий выбирается закон распределения наработки до отказа объекта?

3. В чем заключается постановка задачи при испытаниях объектов на надежность?

4. Что представляет собой процедура формирования статистического ряда по результатам испытаний?

5. Какие эмпирические функции рассчитываются при обработке результатов испытаний?

6. В чем заключается выбор закона распределения наработки до отказа по результатам испытаний?

7. Что представляет собой критерий согласия?

Лекция 6