Средняя наработка до отказа
Рассмотренные выше функциональные показатели надежности P(t), Q(t), f(t) и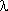 
(t) полностью описывают случайную величину наработки T = {t}. В то же время для решения ряда практических задач надежности бывает достаточно знать некоторые числовые характеристики этой случайной величины и, в первую очередь, среднюю наработку до отказа.
Статистическая оценка средней наработки до отказа
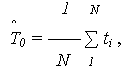
| (1) |
где ti – наработка до отказа i-го объекта.
При вероятностном определении средняя наработка до отказа представляет собой математическое ожидание (МО) случайной величины T и определяется:
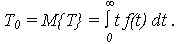
| (2) |
Используя выражение для плотности распределения отказов
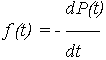
и интегрирование по частям, можно преобразовать (2) к виду
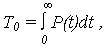
| (3) |
с учетом того, что P(0) = 1, P(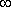 
) = 0.
Из (3) следует, что средняя наработка до отказа геометрически интерпретируется как площадь под кривой P(t) – рис. 1.
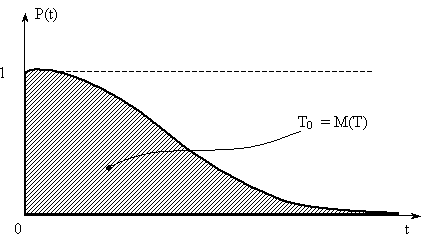
Рис. 1
Очевидно, что с увеличением выборки испытаний N 
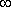средняя арифметическая наработка (оценка 
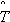0) сходится по вероятности с МО наработки до отказа.
МО наработки T0 означает математически ожидаемую наработку до отказа однотипных элементов, т. е. усредненную наработку до первого отказа.
На практике также представляют интерес условные средние наработки:
1) средняя полезная наработка (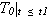 
) определенная при условии, что при достижении наработки t1 все оставшиеся работоспособными объекты снимаются с эксплуатации;
2) средняя продолжительность предстоящей работы (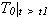 
) при условии, что объект безотказно работал на интервале (0, t1).
Причины использования этих показателей:
1. Высоконадежные объекты (элементы электронных схем), как правило, эксплуатируются меньший срок чем T0 (tэкс < T0), т. е. заменяются по причине морального старения раньше, чем успевают наработать T0.
2. Часто для указанных объектов сокращают период испытаний (проводят до наработок соответствующих их моральному старению), поэтому T0 в таком случае понимают как среднюю наработку, которая имела бы место в действительности, если бы ИО оставалась такой, какой она была в начальный период испытаний.
Средняя полезная наработка 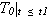(по аналогии с T0):
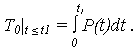
Средняя продолжительность предстоящей работы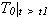
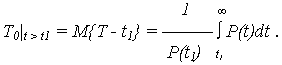
Соотношение между 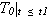, 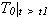и T0:
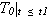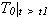+ · P(t1) .
Графические понятия 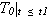и T0|t > t1 иллюстрируются рис. 2.
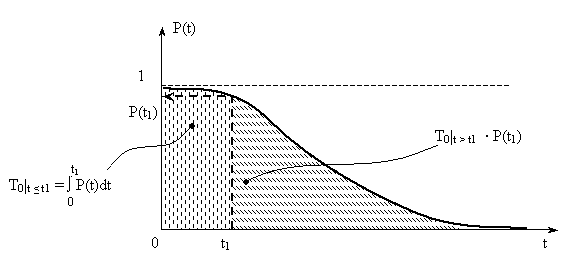
Рис. 2
В то же время средняя наработка не может полностью характеризовать безотказность объекта.
Так при равных средних наработках до отказа T0 надежность объектов 1 и 2 может весьма существенно различаться (рис. 3). Очевидно, что в виду большего рассеивания наработки до отказа (кривая ПРО f2 (t) ниже и шире), объект 2 менее надежен, чем объект 1.
Поэтому для оценки надежности объекта по величине 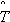0 необходимо еще знать и показатель рассеивания случайной величины T = {t}, около средней наработки T0.
К числу показателей рассеивания относятся дисперсия и среднее квадратичное отклонение (СКО) наработки до отказа.
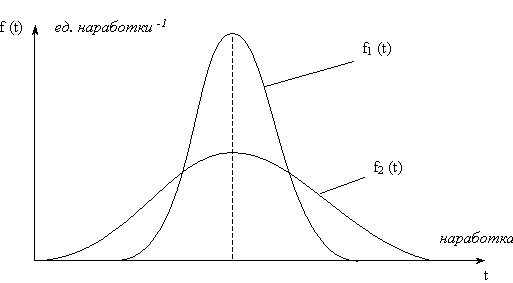
Рис. 3
Дисперсия случайной величины наработки:
- статистическая оценка
| (4) |
- вероятностное определение
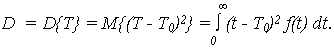
| (5) |
СКО случайной величины наработки:
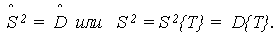
| (6) |
Средняя наработка до отказа T0 и СКО наработки S имеют размерность [ед. наработки], а дисперсия D - [ед. наработки 2].
Контрольные вопросы:
1. Поясните смысл уравнения связи показателей безотказности?
2. Дайте определение статистической оценки и вероятностного представления средней наработки до отказа?
3. Перечислите условные средние наработки до отказа и поясните необходимость их использования?
4. Дайте определение статистических оценок и вероятностного представления характеристик рассеивания случайной величины наработки.
Лекция 5
Дата добавления: 2015-12-08; просмотров: 1814;