Где – коэффициент чистой регрессии при факторе , – средняя квадратическая (стандартная) ошибка коэффициента регрессии .
Для уравнения множественной регрессии 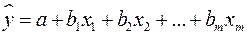 средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:
средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:
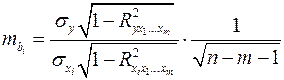 , (2.26)
, (2.26)
Где – среднее квадратическое отклонение для признака , – среднее квадратическое отклонение для признака , – коэффициент детерминации для уравнения множественной регрессии, – коэффициент детерминации для зависимости фактора со всеми другими факторами уравнения множественной регрессии; – число степеней свободы для остаточной суммы квадратов отклонений.
Как видим, чтобы воспользоваться данной формулой, необходимы матрица межфакторной корреляции и расчет по ней соответствующих коэффициентов детерминации 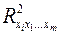 . Так, для уравнения
. Так, для уравнения 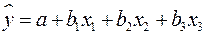 оценка значимости коэффициентов регрессии
оценка значимости коэффициентов регрессии 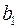 ,
, 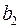 ,
, 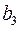 предполагает расчет трех межфакторных коэффициентов детерминации:
предполагает расчет трех межфакторных коэффициентов детерминации: 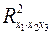 ,
, 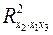 ,
, 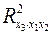 .
.
Взаимосвязь показателей частного коэффициента корреляции, частного -критерия и -критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов. Отсев факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинам и . Частный -критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом.
Пример.Оценим качество уравнения, полученного в предыдущем параграфе. Сначала найдем значения парных коэффициентов корреляции:
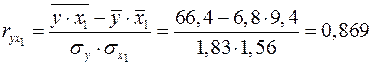 ;
;
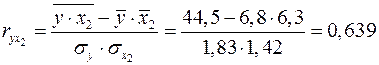 ;
;
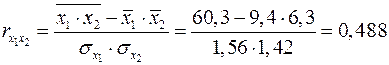 .
.
Значения парных коэффициентов корреляции указывают на достаточно тесную связь сменной добычи угля на одного рабочего 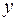 с мощностью пласта
с мощностью пласта 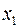 и на умеренную связь с уровнем механизации работ
и на умеренную связь с уровнем механизации работ 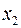 . В то же время межфакторная связь
. В то же время межфакторная связь 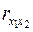 не очень сильная (
не очень сильная ( 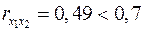 ), что говорит о том, что оба фактора являются информативными, т.е. и
), что говорит о том, что оба фактора являются информативными, т.е. и 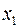 , и
, и 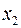 необходимо включить в модель.
необходимо включить в модель.
Теперь рассчитаем совокупный коэффициент корреляции 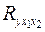 . Для этого сначала найдем определитель матрицы парных коэффициентов корреляции:
. Для этого сначала найдем определитель матрицы парных коэффициентов корреляции:
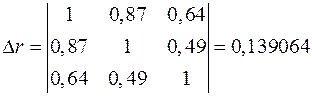 ,
,
и определитель матрицы межфакторной корреляции:
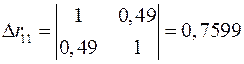 .
.
Тогда коэффициент множественной корреляции по формуле (2.16):
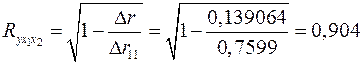 .
.
Т.е. можно сказать, что 81,7% (коэффициент детерминации 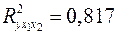 ) вариации результата объясняется вариацией представленных в уравнении признаков, что указывает на весьма тесную связь признаков с результатом.
) вариации результата объясняется вариацией представленных в уравнении признаков, что указывает на весьма тесную связь признаков с результатом.
Примерно тот же результат (различия связаны с ошибками округлений) для коэффициента множественной регрессии получим, если воспользуемся формулами (2.12) и (2.15):
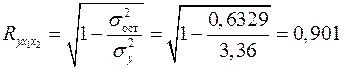 ;
;
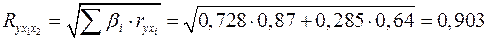 .
.
Скорректированный коэффициент множественной детерминации
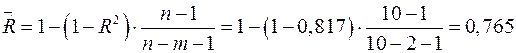
указывает на умеренную связь между результатом и признаками. Это связано с малым количеством наблюдений.
Теперь найдем частные коэффициенты корреляции по формулам (2.18а) и (2.19а):
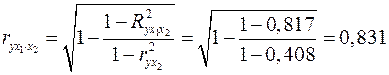 ;
;
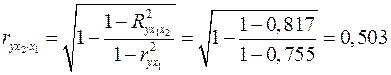 .
.
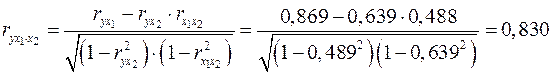 ;
;
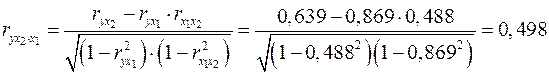 .
.
Т.е. можно сделать вывод, что фактор 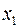 оказывает более сильное влияние на результат, чем признак
оказывает более сильное влияние на результат, чем признак 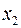 .
.
Оценим надежность уравнения регрессии в целом и показателя связи с помощью 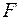 -критерия Фишера. Фактическое значение
-критерия Фишера. Фактическое значение 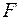 -критерия (2.22)
-критерия (2.22)
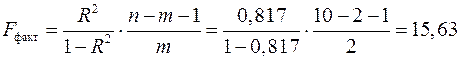 .
.
Табличное значение 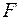 -критерия при пятипроцентном уровне значимости (
-критерия при пятипроцентном уровне значимости ( 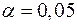 ,
, 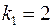 ,
, 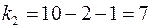 ):
): 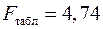 . Так как
. Так как 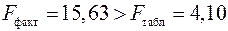 , то уравнение признается статистически значимым.
, то уравнение признается статистически значимым.
Оценим целесообразность включения фактора 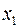 после фактора
после фактора 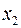 и
и 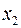 после
после 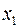 с помощью частного
с помощью частного 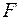 -критерия Фишера (2.23а):
-критерия Фишера (2.23а):
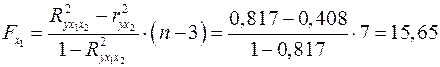 ;
;
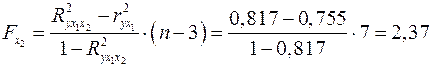 .
.
Табличное значение частного 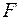 -критерия при пятипроцентном уровне значимости (
-критерия при пятипроцентном уровне значимости ( 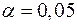 ,
, 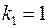 ,
, 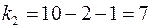 ):
): 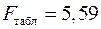 . Так как
. Так как 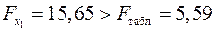 , а
, а 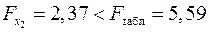 , то включение фактора
, то включение фактора 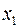 в модель статистически оправдано и коэффициент чистой регрессии
в модель статистически оправдано и коэффициент чистой регрессии 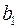 статистически значим, а дополнительное включение фактора
статистически значим, а дополнительное включение фактора 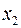 , после того, как уже введен фактор
, после того, как уже введен фактор 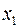 , нецелесообразно.
, нецелесообразно.
Уравнение регрессии, включающее только один значимый аргумент 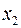 :
:
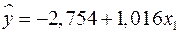 .
.
Дата добавления: 2016-01-29; просмотров: 2022;
