Проверка существенности факторов

И показатели качества регрессии

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – показателя детерминации.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

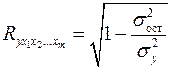, (2.12)

Где – общая дисперсия результативного признака; – остаточная дисперсия.

Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:

.

При правильном включении факторов в регрессионную модель величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем, четвертом знаках). Отсюда ясно, что сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора.

Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:

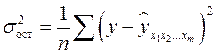. (2.13)

Можно пользоваться следующей формулой индекса множественной детерминации:

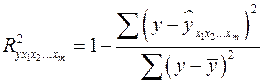. (2.14)

При линейной зависимости признаков формула индекса множественной корреляции может быть представлена следующим выражением:

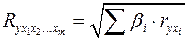, (2.15)