Вероятность отказа как характеристика надежности

Безотказное функционирование трубопроводов, резервуаров и оборудования заключается в способности данной конструкции противостоять отказу в виде потери прочности или местной потери устойчивости оболочки в заданных условиях функционирования.

Оценка безотказности сводится к определению характеристики, количественно оценивающей возможность разрушения или местной потери устойчивости с учетом изменчивости и случайного характера нагрузок и воздействий.

Таким образом, основное средство оценки безотказности - определение вероятности отказа или вероятности безотказной работы.

Безотказность стенки трубы или резервуара, как конструкции, гарантируется на стадии проектирования расчетами на прочность, устойчивость и по деформациям, которые задают необходимые соотношения между параметрами прочности и параметрами нагрузки. Эти соотношения представляют собой неравенства, ограничивающие область безопасных состояний конструкции.

В общем случае, при оценке безотказности существующих конструкций, должно выполняться неравенство:

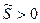(3.1)

При выполнении неравенства (3.1) отказа не произойдет, при невыполнении - произойдет.

Вероятность невыполнения неравенства (3.1) называют вероятностью отказа и обозначают V.

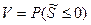- вероятность отказа;

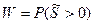- вероятность безотказной работы.

Если V=0, то разрушение конструкции не произойдет ни при каких обстоятельствах. Однако на практике этого достичь не удается, или достигается это при очень больших экономических затратах.

Поэтому назначается какая-то допустимая вероятность отказа, величина которой обосновывается последствиями разрушения конструкции и экономическими соображениями. В общем случае, при любом законе распределения случайных величин, вероятность отказа определяется по формуле:

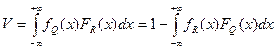, (3.2)

где 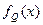, 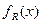- плотности распределения параметров нагрузки и прочности;

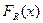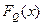, - функции распределения параметров прочности и нагрузки.

При нормальном законе распределения случайных величин 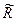и 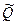вероятность отказа определяется (для положительной числовой полуоси):

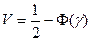, ( 3.3)

где Ф(γ) - интеграл вероятности Гаусса (частный случай нормированной функции Лапласа для положительной числовой полуоси);

γ - характеристика безотказности.

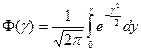; (3.4)

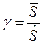, (3.5)

где 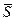- математическое ожидание запаса прочности;

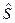– стандарт отклонения запаса прочности, как случайной величины.

Значения интеграла вероятности Ф(γ) приведены в справочниках специальных функций в табличном виде или могут быть определены численными методами.