Методика определения и регулирования вероятности отказа
Последовательность действий по методике, разработанной в теории надежности Ржанициным и другими авторами, заключается в следующем:
1) вычисляются математические ожидания параметров прочности 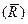 ,параметров нагрузки
,параметров нагрузки 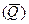 и запаса прочности
и запаса прочности 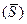 :
:
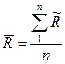 ; (3.6)
; (3.6) 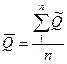 ; (3.7)
; (3.7) 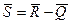 ; (3.8)
; (3.8)
2) вычисляются дисперсии 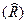 и
и 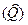 :
:
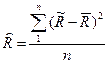 ; (3.9)
; (3.9) 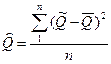 ; (3.10)
; (3.10)
3) вычисляется стандарт отклонения случайных значений запаса прочности:
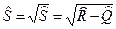 ; (3.11)
; (3.11)
4) определяется характеристика безопасности:
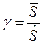 ; (3.12)
; (3.12)
5) по таблице нормированных функций Лапласа определяется величина интеграла вероятностей Гаусса:
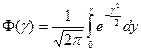 ; (3.13)
; (3.13)
6) вычисляется величина вероятности отказа:
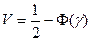 ; (3.14)
; (3.14)
7) проверяется неравенство:
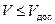 , (3.15)
, (3.15)
где 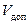 - допускаемая величина вероятности отказа.
- допускаемая величина вероятности отказа.
Если неравенство (3.15) не выполняется, то, так как 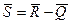 , увеличить характеристику безопасности γ, для чего необходимо либо увеличить параметр прочности
, увеличить характеристику безопасности γ, для чего необходимо либо увеличить параметр прочности 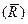 , уменьшить параметр нагрузки
, уменьшить параметр нагрузки 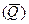 . Есть и другой путь увеличения характеристики безопасности - уменьшение
. Есть и другой путь увеличения характеристики безопасности - уменьшение 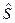 , то есть стандарта отклонения.
, то есть стандарта отклонения.

Рис. 3.1. Сравнение двух материалов по разбросу характеристик прочности
Чтобы уменьшить стандарт отклонения 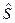 , нужно в формуле (3.11) уменьшить дисперсию параметра прочности
, нужно в формуле (3.11) уменьшить дисперсию параметра прочности 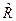 или дисперсию параметров нагрузки
или дисперсию параметров нагрузки 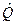 или и то, и другое одновременно.
или и то, и другое одновременно.
На рис. 3.1. приведены плотности распределения параметров прочности 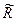 двух марок сталей, имеющих одинаковые математические ожидания, но разный разброс параметров прочности и отличающиеся дисперсии
двух марок сталей, имеющих одинаковые математические ожидания, но разный разброс параметров прочности и отличающиеся дисперсии 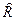 и стандарты отклонения
и стандарты отклонения 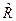 .
.
Сталь 1, характеристики прочности которой имеют дисперсию 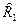 и стандарт отклонения
и стандарт отклонения 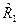 , имеет более однородную структуру и более стабильные механические свойства, по сравнению со сталью 2 с дисперсией
, имеет более однородную структуру и более стабильные механические свойства, по сравнению со сталью 2 с дисперсией 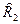 и стандартом отклонения
и стандартом отклонения 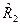
Дата добавления: 2016-01-29; просмотров: 831;
