Кинематический анализ пространственных систем
Как известно, расчетная схема сооружения должна быть геометрически неизменяемой. Многие условия и выводы, полученные при кинематическом анализе плоских систем, применимы и при анализе пространственных систем. Но их недостаточно. Потому вводятся новые понятия и рассматриваются новые способы анализа их геометрической неизменяемости.
Любую геометрически неизменяемую часть пространственной системы будем называть телом. Любое тело без связей имеет шесть степеней свободы – три независимых поступательных перемещения и три поворота. Следовательно, для исключения этих степеней свободы тело нужно закреплять как минимум шестью связями.
Простейший способ закрепления тела к земле показан на рис. 9.3 а, где имеется три типа опор – шаровая подвижная опора A, шаровая опора на цилиндрических катках B и шаровая неподвижная опора C. Из них опора C исключает три поступательных перемещения тела, опора B – два поворота и опора A – один поворот. Таким образом получается геометрически неизменяемая система.
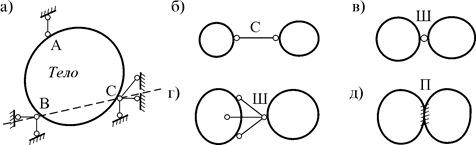
Рис. 9.3
Связи, соединяющие два тела, могут быть разными. Простейшая связь в виде стержня (С) показана на рис. 9.3 б. Если же два тела соединяются шаровым шарниром (рис. 9.3 в), то это соединение эквивалентно трем связям (рис. 9.3 г). Припайка, жестко связывающая два тела (рис. 9.3 д), эквивалентна шести связям.
Если в пространственной системе имеется nТ тел, nШ шаровых шарниров, nC стержней, 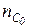 опорных связей и nП припаек, то число степеней свободы такой системы определяется по формуле
опорных связей и nП припаек, то число степеней свободы такой системы определяется по формуле
W = 6nТ – 3nШ – nC – 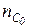 – 6nП .
– 6nП .
Как и для плоской системы, для геометрической неизменяемости пространственной системы необходимо выполнение условия W£0.
Дата добавления: 2016-01-29; просмотров: 826;
