Опоры пространственных систем и их реакции
Пространственные системы опираются на пространственные опоры, которые имеют свои кинематические и статические свойства. Обычно связи опор считаются жесткими, а перемещения по их направлениям равны нулю. При определении опорных реакций используются известные в механике уравнения равновесия.
В отличие от плоских систем опоры пространственных систем могут быть 15 типов. Из них рассмотрим четыре типа опор.
1. Шаровая подвижная опора (рис. 9.2 а). На рисунке изображается как шарик, свободно качающийся между опорной плоскостью и элементом конструкции, а в расчетной схеме – как одна вертикальная связь. У этой опоры имеется пять степеней свободы – она дает возможность поступательных перемещений в двух и поворотов в трех направлениях. В ней возникает только одна опорная реакция 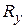 .
.
2. Шаровая опора на цилиндрических катках (рис. 9.2 б). На рисунке изображается как шарик между двумя балансирами, один из которых жестко связан с элементом конструкции, а другой находится на цилиндрических катках. В расчетной схеме изображается в виде двух связей. У этой опоры имеется четыре степени свободы – одно поступательное перемещение и три поворота. В ней возникают две реакции 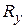 и
и 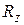 .
.
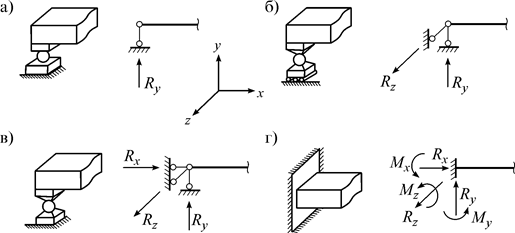
Рис. 9.2
3. Шаровая неподвижная опора (рис. 9.2 в). На рисунке изображается как шарик между двумя балансирами, жестко связанными с элементом конструкции и основанием, а в расчетной схеме в виде трех связей. У этой опоры есть три степени свободы – возможность поворота в трех направлениях. В ней возникают три реакции 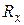 ,
, 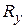 ,
, 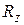 .
.
4. Заделка (рис. 9.2 г). На рисунке изображается как заделанный брус (или стержень), а в расчетной схеме как обычная заделка. У заделки степеней свободы нет. В ней возникают три реакции 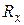 ,
, 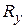 ,
, 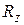 и три реактивных момента
и три реактивных момента 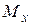 ,
, 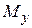 ,
, 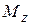 .
.
Кроме рассмотренных здесь, еще имеется 11 различных опор.
Реакции статически определимых пространственных систем определяются из шести уравнений равновесия. Имеется четыре варианта записи этих уравнений, из которых рассмотрим только два:
1. SX=0; SY=0; SZ=0; S 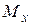 =0; S
=0; S 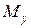 =0; S
=0; S 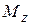 =0.
=0.
Здесь SX, SY, SZ – суммы проекций на три оси x, y, z, которые не должны лежать в одной плоскости и быть параллельными; суммы моментов не обязательно составлять относительно тех же осей.
2. SM1=0; SM2=0; SM3=0; SM4=0; SM5=0; SM6=0.
Здесь 1, 2, …, 6 – шесть любых осей в пространстве. Но:
– эти оси не должны пересекать одну прямую;
– число параллельных осей не должно быть больше трех;
– если три оси пересекаются в одной точке, остальные три не должны быть параллельными.
Дата добавления: 2016-01-29; просмотров: 904;
