Расчет симметричных рам
Симметричными называются системы, расчетные схемы которых симметричны относительно некоторой оси.
Расчет любой симметричной рамы (рис. 8.1 а) можно упростить, если воспользоваться ее симметрией и разложить внешнюю нагрузку на симметричную (рис. 8.1 б) и кососимметричную (рис. 8.1 в) нагрузки.
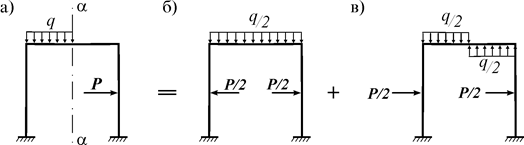
Рис. 8.1
В этом случае, несмотря на то что раму приходится рассчитывать дважды, выбор основной системы, показанной на рис. 8.2 а дает значительный выигрыш в вычислениях.
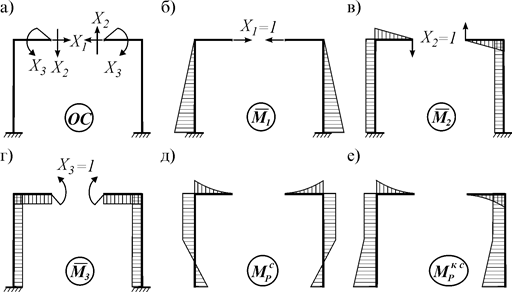
Рис. 8.2
Канонические уравнения будут:
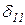 X1+
X1+ 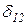 X2+
X2+ 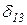 X3+D1P=0,
X3+D1P=0,
 X1+
X1+ 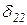 X2+
X2+ 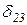 X3+D2P=0,
X3+D2P=0,
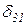 X1+
X1+  X2+
X2+ 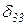 X3+D3P=0.
X3+D3P=0.
Во всех трех единичных состояниях построим эпюры моментов (рис. 8.2 б, в, г). Из них две эпюры (рис. 8.2 б, г) – симметричные, а одна (рис. 8.2 в) – кососимметричная. Симметричная (с) и кососимметричная (кс) эпюры взаимно-ортогональны и их “произведение” равно нулю:
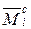 Ä
Ä 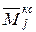 =0.
=0.
Поэтому некоторые коэффициенты системы канонических уравнений обращаются в нуль: 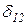 =
=  =0 и
=0 и  =
= 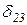 =0, а система канонических уравнений распадается на две независимые системы:
=0, а система канонических уравнений распадается на две независимые системы:

Таким образом, при расчете симметричной рамы некоторые коэффициенты можно не вычислять, а решение большой системы канонических уравнений заменить решением двух систем уравнений значительно меньших размеров.
Дата добавления: 2016-01-29; просмотров: 2253;
