Сущность метода сил
В рассматриваемом методе расчета статически неопределимых систем за основные неизвестные принимаются силы (внутренние усилия). Поэтому он и называется методом сил.
Изучим метод сил на примере предыдущей балки (рис. 7.2 а).
Потребуем, чтобы ее ЗС (рис. 7.2 а) и ОС (рис. 7.2 б) были эквивалентными. Для этого перемещение в направлении исключенной связи должно равняться нулю:
D=0.
По принципу суперпозиции, это перемещение равно сумме перемещения DX (рис. 7.3 а) от неизвестной реакции X и перемещения DP (рис. 7.3 б) от заданной силы P. Поэтому
D=DX+DP=0.
Это уравнение, учитывающее геометрические особенности системы, называется уравнениемсовместности деформаций.

Рис. 7.3
Так как сила X неизвестна, перемещение DX непосредственно определить нельзя. Поэтому рассмотрим единичное состояние (ЕС) основной системы, где действует только единичная сила P=1 (рис. 7.3 в). Перемещение d, возникающее в нем в направлении единичной силы, называется податливостью, и его уже можно определить.
По закону Гука, в линейно-упругой системе DX=d X. Тогда последнее уравнение принимает вид
d X+DP=0.
Его называют каноническим уравнением метода сил. Такое уравнение получается для любой один раз статически неопределимой системы. Если известны d и DP, из него определяется неизвестная сила: X= –DP/d .
Если в системе имеется n лишних связей, то нужно исключить все эти лишние связи и выбрать ОС с n неизвестными X1, X2, ..., Xn. Тогда, из условий эквивалентности ЗС и ее ОС (условий равенства нулю перемещений в направлениях исключенных связей) можно составить n уравнений совместности деформаций:
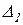 =
= 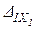 +
+ 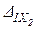 +×××+
+×××+ 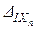 +D1P=0,
+D1P=0,
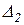 =
= 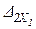 +
+ 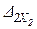 +×××+
+×××+ 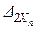 +D2P=0,
+D2P=0,
. . . . . . . . . . . . . .
Dn= 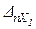 +
+ 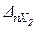 +×××+
+×××+ 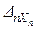 +DnP =0.
+DnP =0.
При рассмотрении n различных единичных состояний системы и определении податливостей 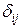 по различным направлениям эти уравнения приводятся к системе уравнений:
по различным направлениям эти уравнения приводятся к системе уравнений:
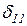
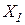 +
+ 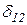 X2+×××+
X2+×××+ 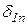 Xn+D
Xn+D 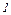 P=0,
P=0,
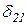
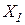 +
+ 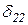 X2+×××+
X2+×××+ 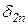 Xn+D2P=0,
Xn+D2P=0,
. . . . . . . . . . . . .
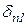
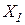 +
+ 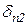 X2+×××+
X2+×××+ 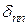 Xn+DnP=0.
Xn+DnP=0.
Она называется системой канонических уравнений метода сил. Здесь 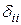 – главные коэффициенты,
– главные коэффициенты, 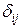 – боковые коэффициенты. Свободные члены DiP называются грузовыми коэффициентами.
– боковые коэффициенты. Свободные члены DiP называются грузовыми коэффициентами.
Систему с большим количеством уравнений необходимо решать на компьютере. С этой целью введем матричные обозначения:
 d=
d= 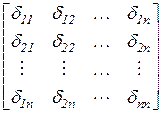 ; X =
; X = 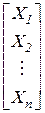 ;DP =
;DP = 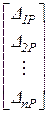 ; 0 =
; 0 = 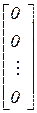 ,
,
где d – матрица податливости, X – вектор неизвестных, DP – вектор нагрузки, 0 – нуль-вектор. В результате этого система канонических уравнений принимает вид:
d X +DP = 0.
Из этого матричного уравнения определяется вектор неизвестных:
X =–d–1DP.
Здесь d–1 – обратная матрица податливости.
Дата добавления: 2016-01-29; просмотров: 790;
