Алгоритм метода Гомори

1. Решаем задачу симплекс методом. Если найденное решение целочисленно, то задача решена. Если задача не разрешима, то она не имеет решений и в целых числах.

2. Если среди компонент оптимального решения есть не целые, то надо выбрать компоненту с оптимальной целой частью и сформулировать правильное отсечение из условия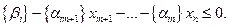

3. Вводим дополнительную неотрицательную целую переменную 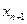и получаем новое уравнение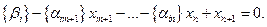

4. Полученную расширенную задачу решаем симплекс-методом. Если новый найденный план целочисленный, то задача решена, если нет то повторяем процедуру.

Замечание. 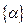- дробная часть числа .

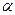Если задача разрешима в целых числах, то после конечного числа шагов (итераций) оптимальный целочисленный план будет найден. Если в процессе решения появится уравнение, выражающее основную переменную через неосновные, в котором свободный член не целый, а все остальные коэффициенты целые, то задача в целых числах решений не имеет. В симплекс таблице это условие соответствует тому, что в строке с нецелым свободным членом все остальные коэффициенты целые.

Пример. Решить задачу в целых числах.

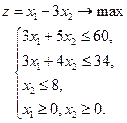
Приведем задачу к каноническому виду:

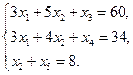
Построим симплекс-таблицу

Базис	Свободный	Переменные	Оценочные
	член						отношения
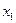
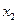
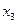
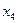
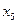
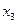
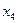
							17/2
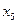
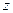
	О	-2	-3

Данный план не оптимален, так как в оценочной строке есть отрицательные элементы. Наибольший по модулю находится в столбце 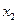. Следовательно 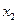переменная вводимая в базис. Построим оценочные отношения. Наименьшее соответствует строке 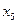. Значит 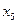вводимая в базис переменная. Переходим к новой симплекс-таблице.

Базис	Свободный	Переменные	Оценочные
	член						отношения
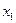
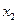
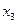
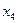
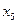
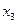
						-5	20/3
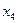
						-4	2/3
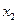
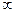
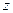
		-2

Полученное решение не является оптимальным. 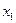вводимая, 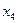выводимая переменная. Переходим к новой симплекс-таблице

Базис	Свободный	Переменные	Оценочные
	член		отношения
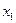
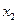
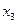
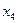
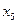
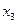
					-1	-1
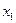
	2/3				1/3	-4/3
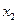
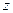
	76/3				2/3	1/3

Полученное решение 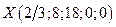оптимально, но не является цело

численным .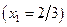

Построим правильное отсечение из условия:

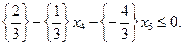
Найдем дробные части от чисел стоящих в фигурных скобках:

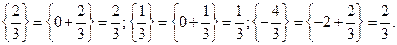
Получим неравенство

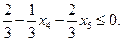
Введем дополнительную целую переменную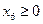

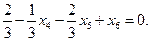
Полученное уравнение необходимо добавить в систему ограничений и решить

симплекс-методом новую задачу.

Для сокращения числа шагов можно вводить новое уравнение в симплекс-таблицу, полученную на последнем шаге.

Базис	Свободный	Переменные	Оценочные
	член							отношения
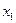
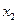
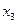
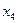
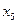
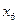
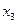
					-1	-1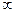
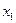
	2/3				1/3	-4/3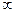
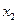
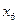
	2/3				1/3	2/3	-1
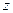
	76/3				2/3	1/3

Полученное базисное решение не допустимо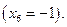

Замечание. Включение в систему ограничений дополнительного ограничения, соответствующего правильному отсечению всегда дает недопустимое базисное решение.

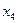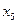Для получения допустимого базисного решения необходимо перевести в основные переменные переменную, входящую со знаком «+» в уравнение, в котором свободный член отрицательный. В рассматриваемом случае это переменная или . Введем .

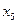Базис	Свободный	Переменные	Оценочные
	член							отношения
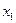
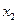
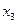
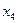
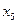
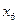
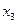
					-1/2		-2/3
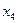
							-2
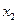
					-1/2		3/2
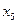
					1/2		3/2
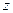
					1/2		1/2

Полученное решение является оптимальным. Найденный план целочисленный