Основные теоремы теории двойственности линейного программирования
Первая (основная) теорема двойственности:если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая задача, причем оптимальные значения их целевых функций равны: 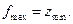 Если область допустимых решений одной из задач неограниченна, то условия другой задачи противоречивы.
Если область допустимых решений одной из задач неограниченна, то условия другой задачи противоречивы.
Замечание. Обратное утверждение не верно. Если условия одной задачи противоречивы, это не вообще говоря не означает, что другая задача неограниченна.
Экономический смысл первой теоремы двойственности. План производства 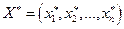 и набор оценок ресурсов
и набор оценок ресурсов 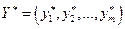 оказываются оптимальными тогда и только тогда, когда прибыль от продукции, найденная по «внешним», заранее известным ценам
оказываются оптимальными тогда и только тогда, когда прибыль от продукции, найденная по «внешним», заранее известным ценам 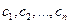 равна затратам на ресурсы по «внутренним», определенным в процессе решения, ценам
равна затратам на ресурсы по «внутренним», определенным в процессе решения, ценам 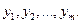 Для всех других планов Х и У прибыль всегда меньше (или равна) затратам на ресурсы, т.е. предприятию безразлично производить ли продукцию по оптимальному плану
Для всех других планов Х и У прибыль всегда меньше (или равна) затратам на ресурсы, т.е. предприятию безразлично производить ли продукцию по оптимальному плану 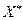 или продавать ресурсы по оптимальным ценам
или продавать ресурсы по оптимальным ценам 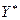 . Прибыль и в том и в другом случае одинакова.
. Прибыль и в том и в другом случае одинакова.
Тесная связь между двумя двойственными задачами проявляется не только в равенстве оптимальных значений их целевых функций. Если каждую из двойственных задач решать симплекс-методом, то их необходимо привести к каноническому виду. Для этого в первой задаче вводятся т неотрицательных переменных 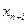 ,
, 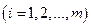 , а во второй задаче п неотрицательных переменных
, а во второй задаче п неотрицательных переменных 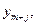
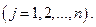 Системы ограничений принимают вид:
Системы ограничений принимают вид:
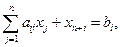
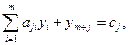
| Переменные исходной задачи | |||||||
| Первоначальные переменные | Дополнительные переменные | ||||||
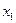
| 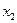
| 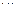
| 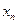
| 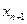
| 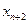
| 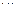
| 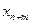
|
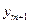
| 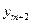
| 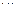
| 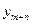
| 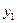
| 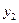
| 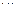
| 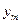
|
| Переменные двойственной задачи |
Теорема. Положительным (не нулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых i выполнено: если 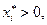 то
то 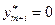 и если
и если 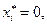 то
то 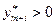 и аналогично для любых i выполнено: если
и аналогично для любых i выполнено: если 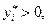 то
то 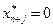 и если
и если 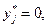 то
то 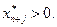
Вторая теорема двойственности.Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции, выраженной через не основные переменные, ее оптимального решения
Пример. Если в исходной задаче на последнем шаге выполнения симплекс-метода
получили: 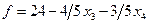 и
и 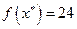 - максимум функции, оптимальное решение
- максимум функции, оптимальное решение 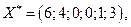 то в двойственной задаче будем иметь:
то в двойственной задаче будем иметь: 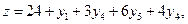
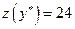 - минимум функции, а оптимальным решением будет:
- минимум функции, а оптимальным решением будет: 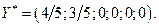 Соответствие между переменными выражается таблицей:
Соответствие между переменными выражается таблицей:
| Переменные исходной задачи | |||||
| Первоначальные переменные | Дополнительные переменные | ||||
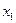
| 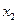
| 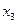
| 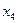
| 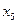
| 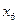
|
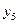
| 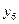
| 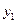
| 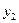
| 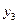
| 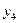
|
| Переменные двойственной задачи |
Замечание. Если в одной из двойственных задач нарушается единственность оптимального решения, то оптимальное решение двойственной задачи вырожденно.
Метод, при котором сначала симплекс-методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находится с помощью теорем двойственности, называется двойственным симплекс методом. Он применяется в случаях, когда первое базисное решение недопустимо или 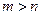 .
.
Дата добавления: 2015-11-28; просмотров: 1763;
