Метод ветвей и границ.
Метод ветвей и границ - один из комбинированных методов решения задач целочисленного линейного программирования. Его суть состоит в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.
Метод ветвей и границ состоит в следующем: множество допустимых решений некоторым образом разбивается на подмножества, каждое из которых этим же способом разбивается еще на подмножества. Процесс продолжается до тех пор, пока не будет найден оптимальный план.
Пусть задача целочисленного линейного программирования решена симплекс-методом без учета целочисленности и известны верхняя и нижняя граница для каждой целой переменной 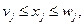
 и нижняя граница целевой функции
и нижняя граница целевой функции 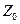 :
: 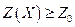 для любого плана Х.
для любого плана Х.
Предположим, что компонента решения оптимального плана 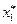 не удовлетворяет условию целочисленности. Тогда из области допустимых решений исключается область
не удовлетворяет условию целочисленности. Тогда из области допустимых решений исключается область 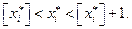
Начальная задача распадается на две (2) и (3). В задачу (2) добавится ограничение  , а в задачу (3) добавится ограничение
, а в задачу (3) добавится ограничение 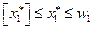 .
.
Решаются задачи (2) и (3). В результате список задач может либо расшириться, либо уменьшиться. Если в результате решения задач (2) или (3) получаем нецелочисленный оптимальный план, при котором 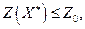 то эта задача исключается. Если
то эта задача исключается. Если  то из данной задачи формируются две новые.
то из данной задачи формируются две новые.
Если полученное решение 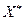 удовлетворяет условию целочисленности и
удовлетворяет условию целочисленности и 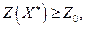 то значение
то значение 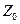 исправляется и за величину
исправляется и за величину 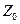 принимается оптимум линейной функции полученного оптимального целочисленного плана.
принимается оптимум линейной функции полученного оптимального целочисленного плана.
Процесс продолжается до тех пор, пока весь список задач не будет исчерпан, то есть все задачи будут решены.
Пример. Решить задачу в целых числах.

В качестве 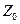 принимаем значение целевой функции в точке
принимаем значение целевой функции в точке 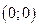
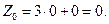
Решим задачу симплекс-методом. Получим 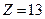
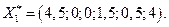 Так как первая компонента
Так как первая компонента 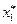 дробная, то из области допустимых решений исключим полосу
дробная, то из области допустимых решений исключим полосу 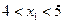 . Получим две задачи:
. Получим две задачи:
| Задача 2 | Задача 3 |
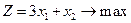
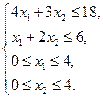
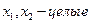
| 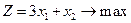
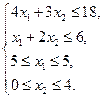
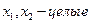
|
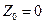
Решим задачу (3) симплекс-методом. Условия задачи (3) противоречивы. Решаем задачу (2). Имеем 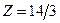
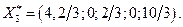 Хотя
Хотя 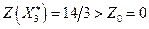 по прежнему сохраняем
по прежнему сохраняем 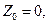 так как план
так как план 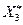 не целочисленный. Величина
не целочисленный. Величина 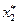 -дробная, следовательно, исключаем полосу
-дробная, следовательно, исключаем полосу 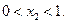
| Задача 3 | Задача 4 |
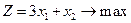
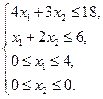
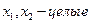
| 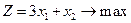
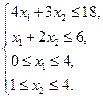
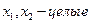
|
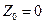
Решаем задачу (4). Имеем 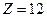
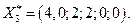 Эту задачу исключаем из списка,
Эту задачу исключаем из списка,
но меняем  Решаем задачу (5). Имеем
Решаем задачу (5). Имеем 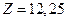
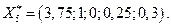 Значение
Значение 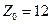 не меняем, так как план не целочисленный. Исключаем полосу
не меняем, так как план не целочисленный. Исключаем полосу 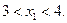 Получаем
Получаем
| Задача 6 | Задача 7 |
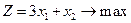
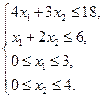
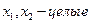
| 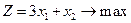
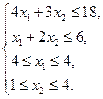
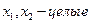
|
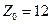
Решаем задачу (7) симплекс-методом. Условия задачи (7) противоречивы. Решаем задачу (6). Имеем 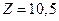
 Значение
Значение 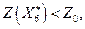 следовательно, задача исключается из списка.
следовательно, задача исключается из списка.
Список задач полностью исчерпан. Получен оптимум 
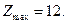
Дата добавления: 2015-11-28; просмотров: 1071;
