Группировка неизвестных

Если при расчете симметричной рамы (рис. 8.3 а) выбрана обычная основная система (рис. 8.3 б), то все коэффициенты канонических уравнений

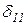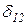X₁+ X₂ +D_1P=0,

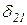X₁+ 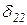X₂ +D_2P=0

будут отличаться от нуля.

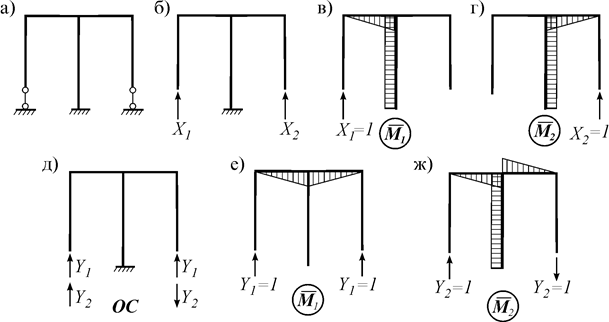
Рис. 8.3

Если же неизвестные группировать по формулам

X₁=Y₁ +Y₂ ,

X₂=Y₁ – Y₂ ,

что соответствует основной системе на рис. 8.3 д, то единичные эпюры (рис. 8.3 е, ж) будут ортогональными ( 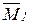Ä 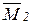=0), и канонические уравнения распадутся на два независимых уравнения:

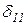Y₁ +D_1P=0,

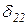Y₂ +D_2P=0.

Как видим, при группировке неизвестных отдельные коэффициенты обращаются в нуль и нет необходимости их вычисления. С другой стороны, распадение системы канонических уравнений на две независимые системы уравнений упрощает их решение. Поэтому группировка неизвестных позволяет существенно уменьшить объем вычислений.

В о п р о с ы

1. Какие существуют способы проверки коэффициентов канонических уравнений?

2. В чем заключается универсальная проверка?

3. Для чего используется постолбцовая проверка?

4. Каков алгоритм метода сил?

5. Какие способы проверки правильности расчета существуют?

6. Какие три способа применяются при определении перемещений статически неопределимых систем?

7. Какие системы называются симметричными?

8. Какое преимущество дает использование симметрии рамы?

9. В чем состоит группировка неизвестных?

Л е к ц и я 9