Аксонометрия и ее свойства.
Аксонометрия представляет собой способ построения изображения. Пусть в пространстве дан аффинный репер R (O¢, E1¢, E2¢, E3¢). С ним связана аффинная система координат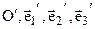 
.
Решение задачи построения изображения точки, если даны ее координаты в пространстве
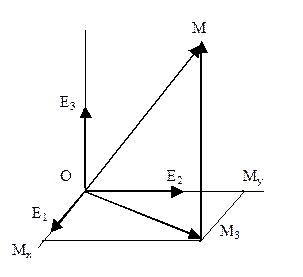
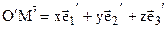
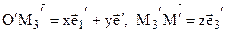
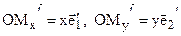
М3 – вторичная проекция точки.
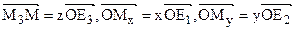
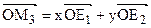
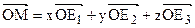
Триметрические, диметрические и изометрические проекции.
Триметрическая проекция – все три коэффициента искажения различны между собой
Диметрическая проекция – два коэффициента искажения равны между собой, а третий отличен от них.
 |
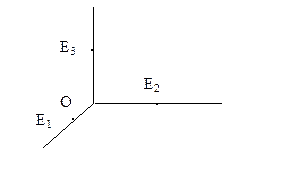Изометрическая проекция – все коэффициенты искажения равны между собой.
Кабинетная проекция
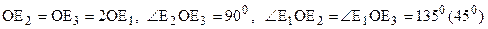
Кавальерная или военная проекция.
 |
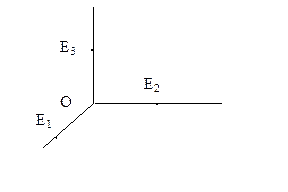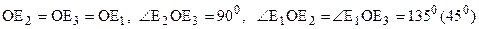
Задачи аксонометрии.
Дана точка (М, М3) построить ее вторичные проекции M1 и М2 на плоскости Oyz и Оxz.
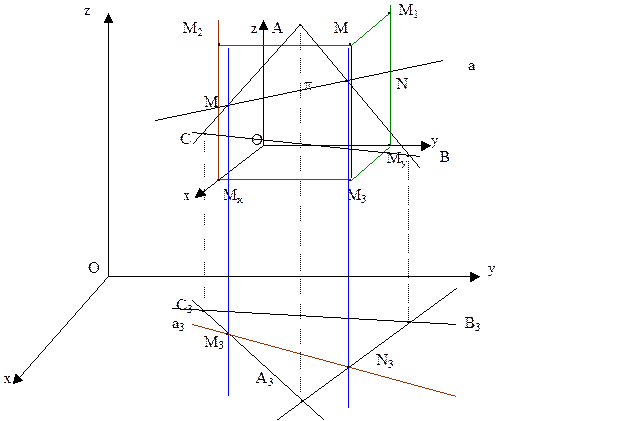
Прямая (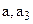 
) лежит в плоскости, определяемой точкам 
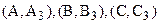. Найти ее проекцию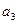 
Дана аксонометрическая проекция точки М, лежащей в плоскости p, которая в свою очередь определена следом р3 на плоскости Оху и точкой (РО) ее пересечения с осью Оz. Найти вторичную проекцию М3.
 |
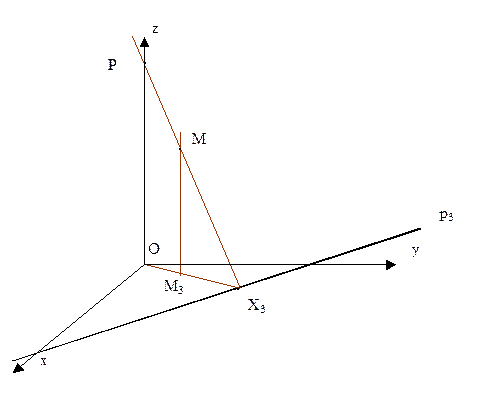Полные и неполные изображения.
 |
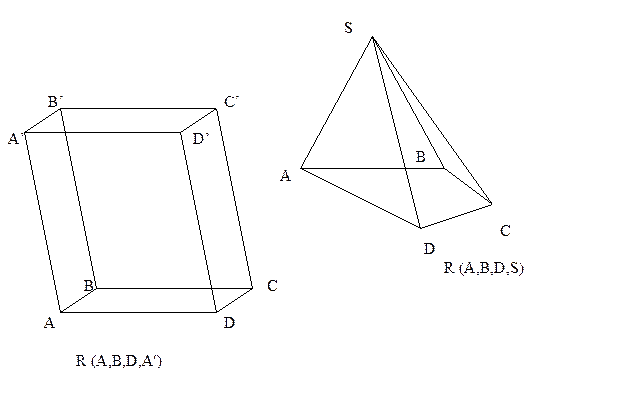Изображение называется полным, если к нему можно присоединить изображение репера так, что все его точки будут определены.
Пример неполного изображения
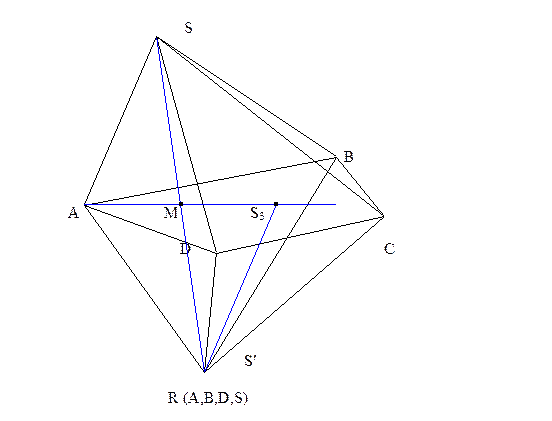
Аффинные задачи аксонометрии.
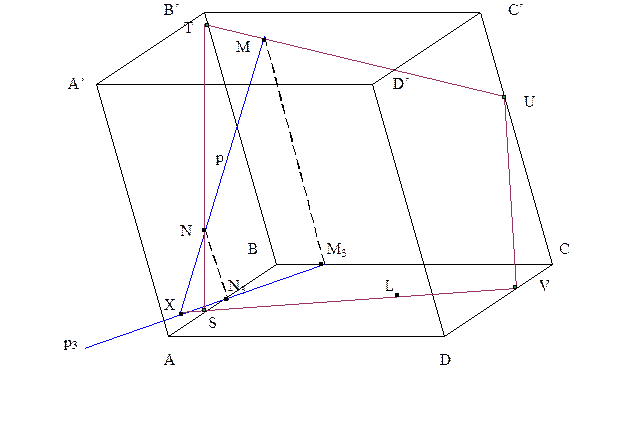
Дан параллелепипед ABCDA¢B¢C¢D¢, точки L, M и N расположены соответственно на гранях ABCD, BB¢C¢C и ABB¢A¢. Построить сечение параллелепипеда плоскостью LMN.
Дан тетраэдр ABCS. Даны точки М, N и P, принадлежащие соответственно боковым граням SBC, SAC и SAB. Построить сечение тетраэдра плоскостью MNP.
 |
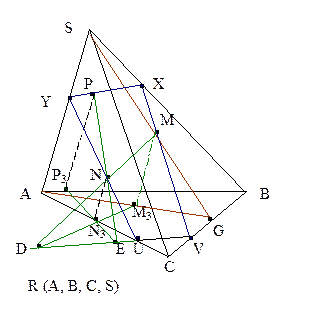МЕТРИЧЕСКИЕ ЗАДАЧИ АКCОНОМЕТРИИ
Аффинный репер R=(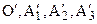 
) называется декартовым, если известны длины базисных векторов 
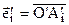и угол между ними. 
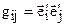- 6 независимых параметров.
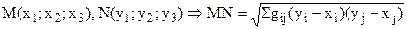
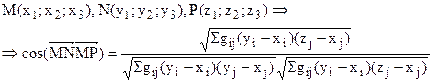
Метрически и евклидово определенные изображения.
Аффинный репер R=( 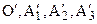) называется метрически определенным, если известны все параметры, определяющие попарные произведения всех его векторов. Репер называется евклидово определенным, если известно такое число параметров, которое определяет репер с точностью до подобия в пространстве, например, отношение скалярных произведений.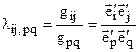 
5 независимых параметров:
.
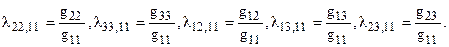
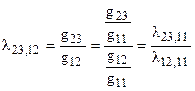На плоскости метрически определенный репер - 3 параметра, евклидово определенный – 2 параметра.
В евклидово определенном репере можно найти отношение длин отрезков и углы между векторами.
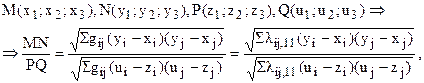
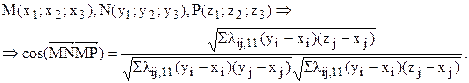
Задача 1. Дано изображение равнобедренного треугольника с углом при основании в 300. Построить изображение высоты, опущенной на его боковую сторону.
Изображение евклидово определенное. Отношение боковых сторон равно1, угол между ними - 1200
Задача. На плоскости даны параллелограмм ABCD, луч и отрезок, которые являются изображением квадрата, луча и отрезка, лежащих в одной плоскости. Построить на данном луче изображение отрезка, равного данному.
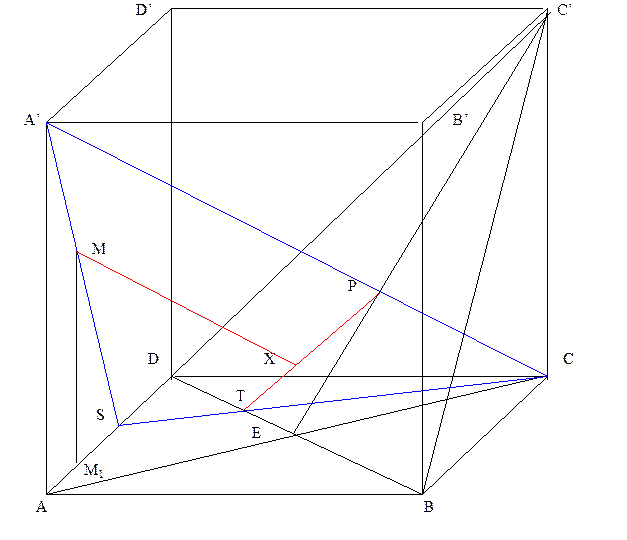
Задача. Дан куб ABCDA’B’C’D’, на грани AA’D’D дана точка М. Опустить из этой точки перпендикуляр на плоскость BC’D
Дата добавления: 2016-02-02; просмотров: 3205;