Бином Ньютона и его свойства.
ОСНОВНЫЕ ПОНЯТИЯ КОМБИНАТОРИКИ.
n – факториал ‒ произведение первых n ‒ натуральных чисел(обозначается n!).
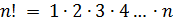
Основными понятиями комбинаторики являются ‒ размещения, перестановки и сочетания.
Определение 1.Пусть имеется множество, содержащее n‒элементов.
Размещением из n ‒ элементов по m ‒ элементов (m≤n) ‒ называются все подмножества, содержащие m ‒ элементов и отличающиеся друг от друга или составом своих элементов или порядком их следования.
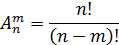
‒ число размещений из n ‒ элементов по m ‒ элементов.
Определение 2.Перестановками из n ‒ элементов называются размещения из n ‒ элементов по n ‒ элементов.
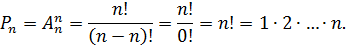
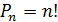 –число перестановок из n ‒ элементов.
–число перестановок из n ‒ элементов.
Определение 3.Сочетаниями из n ‒ элементов по m ‒ элементов(m≤n) называются все m‒ элементные подмножества n ‒ элементного множества, отличающиеся друг от друга только составом своих элементов.
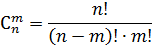
‒ число сочетаний из n ‒ элементов по m ‒ элементов.
Свойства сочетаний:
1. 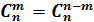
Доказательство:
Так как
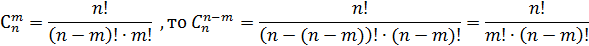
Следовательно,
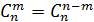
Примеры:
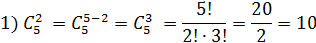
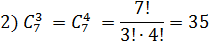
2. 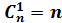
Доказательство:
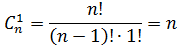
Примеры:
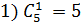
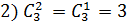
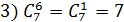
3. 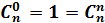
Доказательство:
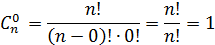
Примеры:
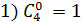
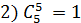
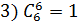
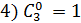
Бином Ньютона и его свойства.
Воспользуемся формулами:
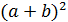 =
= 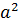 +2ab+
+2ab+ 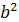 =
= 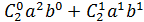 +
+ 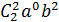
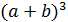 =
= 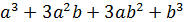 =
= 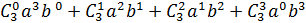
Используя принцип математической индукции(от частных примеров к общей формуле) получим формулу Ньютона:
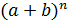 =
= 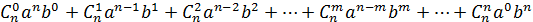
Или кратко:
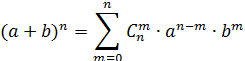
– формула Ньютона для степени бинома или бином Ньютона.
Свойства:
1. Формула содержит (n+1)‒ слагаемое.
2. Показатель степени a‒ убывает от n до 0; Показатель степени b – возрастает от 0 до n.
3. Любой член разложения можно найти по формуле:
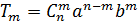 .
.
4. Коэффициенты 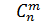 называются – биноминальными. Биноминальные коэффициенты, равноудаленные от концов разложения, равны между собой.
называются – биноминальными. Биноминальные коэффициенты, равноудаленные от концов разложения, равны между собой.
5. Сумма всех биноминальных коэффициентов находятся по формуле:
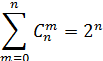
Доказательство:
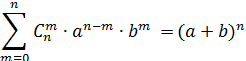
Пусть a=b= 1.
Тогда
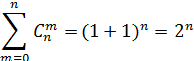
Примеры на формулу Ньютона и ее свойства:
Пример 1.
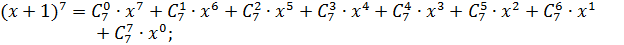
Где 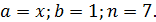
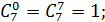
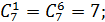
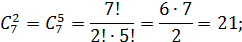
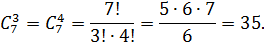
Следовательно,
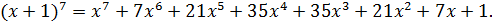
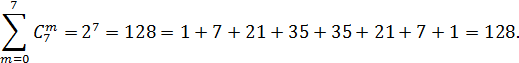
Пример 2.
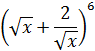
Найти: 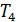 .
.
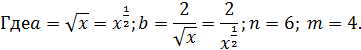
Решение:
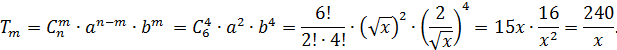
В комбинаторных задачах удобно пользоваться следующей таблицей:
| Выбор | Сочетания | Размещение | Перестановка |
| Без повторения | 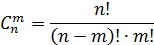
| 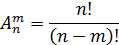
| 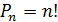
|
| С повторением | 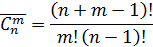
| 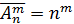
| 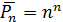
|
Дата добавления: 2015-12-16; просмотров: 8433;
