Зависимые события. Вероятность произведения зависимых событий.
События A и B называются зависимыми, если вероятность одного из них зависит от того, произошло или не произошло другое событие.
Рассмотрим пример.
В коробке находится a белых и b черных шаров. По очереди один за другим извлекаются 2 шара и назад не кладутся.
Обозначим случайные события:
A‒1‒й шар белый;
B‒ 2‒й шар белый.
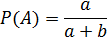
Если событие A не произошло, то вероятность событияB.
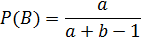
Если событие A произошло, то есть первый шар белый, тогда
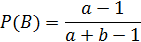
Определение.Вероятность события B, вычисленная при условии, что событие A произошло, называется условной вероятностью, и обозначается 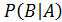 или
или 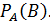
Для условной вероятности имеют место формулы:
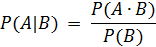
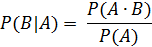
Теорема 4. Вероятность произведения зависимых событий равна произведению вероятности одного из них на условную вероятность другого события, вычисленную при условии, что первое событие произошло.
Теорема следует из предыдущих формул:
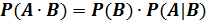
или
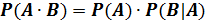
Распространим эту теорему на любое число зависимых событий:
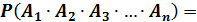
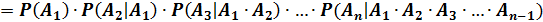
Пример.
На складе 20 мешков с мукой высшего сорта,12 мешков первого сорта, 5 мешков второго сорта. По очереди один за другим достают 3 мешка с мукой и назад не возвращают.
Найти вероятность того, что первый мешок с мукой высшего сорта (событие 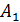 ). Второй мешок с мукой первого сорта (событие
). Второй мешок с мукой первого сорта (событие 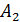 ). Третий мешок с мукой второго сорта (событие
). Третий мешок с мукой второго сорта (событие 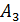 ).
).
Решение:
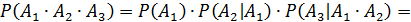
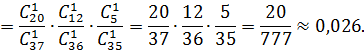
Дата добавления: 2015-12-16; просмотров: 1332;
