Лекция 4.ОСНОВНЫЕ ФОРМУЛЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.
Формула полной вероятности.
Теорема 1.Вероятность события A, вычисленная при условии осуществления одного из несовместных событий H1,H2,H3,., Hn , образующих полную группу, находится по формуле:
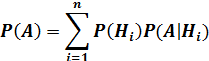
‒ формула полной вероятности.
Где  события ‒ гипотезы.
события ‒ гипотезы.
Доказательство:
Так как событие A, может произойти только с одним из несовместных событий или  или
или 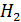 , или
, или 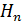 , то
, то
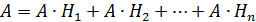
Тогда по теореме о вероятности произведения зависимых событий, получим:
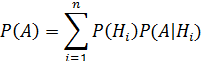
Пример 1.
Партия деталей изготавливается тремя рабочими. Причем первый рабочий изготовил 25% деталей. Второй 35% деталей. Третий 40% деталей. В продукции первого рабочего брак составляет 5%. У второго рабочего брак составляет 4%.У третьего рабочего брак составляет 2%. Найти вероятность того, что случайно выбранная для контроля деталь окажется бракованной.
Решение:
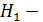 деталь изготовил первый рабочий.
деталь изготовил первый рабочий.
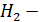 деталь изготовил второй рабочий.
деталь изготовил второй рабочий.
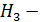 деталь изготовил третий рабочий.
деталь изготовил третий рабочий.
A ‒ взятая деталь бракованная.
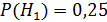

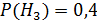

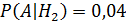
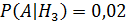
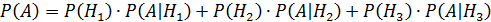

Формула Байеса.
Пусть событие A может произойти с одним из несовместимых событий 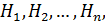 образующих полную группу, тогда
образующих полную группу, тогда
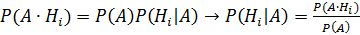 или
или
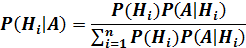
‒ формула Байеса.
Пример.
В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Телевизоры от первого, второго и третьего поставщиков не потребуют ремонта в течение гарантийного срока, в следующих 98%, 88% и 92% случаях.
Найти:
1. Вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока (событие A).
2. Вероятность того, что проданный телевизор потребовал ремонта в течение гарантийного срока (событие B). От какого поставщика вероятнее всего этот телевизор.
Решение:
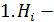 телевизор поступил от i ‒ й фирмы. i= 1, 2, 3.
телевизор поступил от i ‒ й фирмы. i= 1, 2, 3.
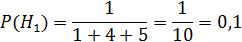
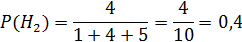
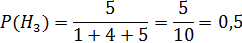
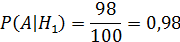
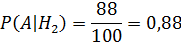
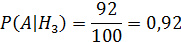
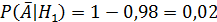

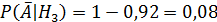
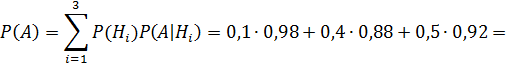
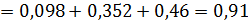
2. 
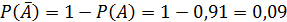
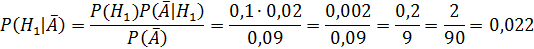


Ответ: вероятнее всего брак второй фирмы, так как брак второй фирмы составил максимальную вероятность равную 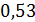 .
.
Дата добавления: 2015-12-16; просмотров: 1441;
