Повторение независимых испытаний. Формула Бернулли.
Пусть производится серия из n-независимых испытаний (опытов), в каждом из которых событие A наступает с вероятностью р. Тогда вероятность того, что событие A не произойдет, обозначим q=1 - p.
Вероятность того, что при n-испытаниях событие произойдет ровно m-раз, находится по формуле Бернулли:
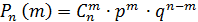
- формула Бернулли.
Пример.
Вероятность попадания мяча в кольцо составляет 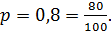
Вероятность промаха мяча в кольцо составляет 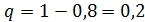
Найти:
1. Вероятность того, что при 7 бросках мяч попадет 4 раза (событие A).
2. Вероятность того, что мяч попадет не менее 4-х раз, то есть 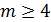 или
или 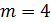 , или
, или 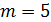 ,или
,или 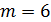 ,или
,или 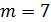 .
.
Решение:
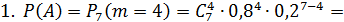
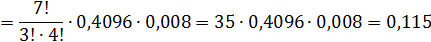
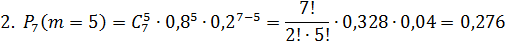
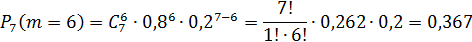
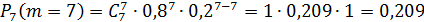
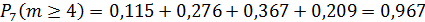
Наивероятнейшее число наступлений события (число успехов).
Определение. Число 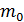 наступления события A в n-независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события, по крайней мере, не меньше вероятностей других событий.
наступления события A в n-независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события, по крайней мере, не меньше вероятностей других событий.
Наивероятнейшее число 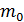 наступления события (число успехов)удовлетворяет следующему неравенству:
наступления события (число успехов)удовлетворяет следующему неравенству:
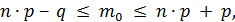
где 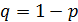 ;
; 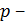 вероятность наступления события в отдельных испытаниях.
вероятность наступления события в отдельных испытаниях.
Пример. Вероятность изготовления на автоматическом станке стандартной детали 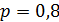 . Найти вероятности возможного числа появления бракованных деталей среди пяти отобранных и выбрать среди них наивероятнейшее число.
. Найти вероятности возможного числа появления бракованных деталей среди пяти отобранных и выбрать среди них наивероятнейшее число.
Решение:
1 способ.
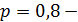 вероятность изготовления стандартной детали.
вероятность изготовления стандартной детали.
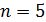 ;
; 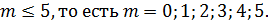
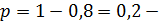 вероятностьпоявления брака.
вероятностьпоявления брака.
Тогда 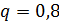
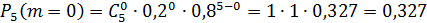
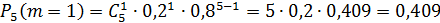
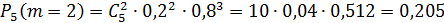
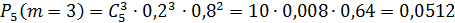
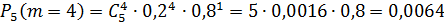
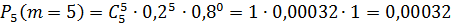
Следовательно, наивероятнейшее число бракованных деталей 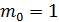 .
.
2способ.
Оценим 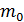 с помощью неравенства:
с помощью неравенства:
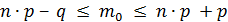
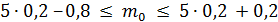
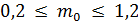
Следовательно, 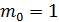 ,
, 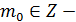 множество целых чисел.
множество целых чисел.
Дата добавления: 2015-12-16; просмотров: 1103;
