ДЛЯ КВАДРАТИЧНОЙ ОБЛАСТИ СОПРОТИВЛЕНИЯ. ФОРМУЛА ШЕЗИ. МОДУЛЬ РАСХОДА И МОДУЛЬ СКОРОСТИ
При проектировании гидротехнических сооружений обычно сталкиваются с квадратичной областью сопротивления, когда вода имеет достаточно большие скорости, при которых числа Рейнольдса получаются также достаточно большими.
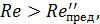 (4-92)
(4-92)
где 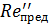 имеет тот же смысл, что и
имеет тот же смысл, что и 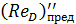 в предыдущем параграфе.
в предыдущем параграфе.
Очень часто при условии, когда неравенство (4-93) несколько нарушается, т. е. когда мы, строго говоря, получаем доквадратичную область сопротивления, практические расчеты все же ведут по зависимостям, относящимся к квадратичной области. Это объясняется тем, что расчет для области квадратичного сопротивления является значительно более простым, чем для области доквадратичного сопротивления. Действительно, для доквадратичной области коэффициент λ, входящий в формулу (4-69), зависит от Re, а следовательно, и от скорости v, которая часто заранее неизвестна. В связи с этим задачи для доквадратичной области обычно приходится решать путем подбора или методом последовательного приближения. В случае же области квадратичного сопротивления λ не зависит от Re, а следовательно, λмы можем найти, не зная величины v, что обычно позволяет решать задачи непосредственно, без подбора. Вместе с тем погрешность в определении величины λ, обусловленная пренебрежением влияния на нее числа Re (когда мы находимся в доквадратичной области), часто может быть значительно меньше той погрешности, которая получается за счет неточности установления величины Δ: как мы видели, шероховатость Δ приходится устанавливать по таблице, где этот параметр определяется на основании чисто описательных, качественных (а не количественных) характеристик русла.
Перечисленные обстоятельства заставляют в гидротехнической практике интересоваться главным образом областью квадратичного сопротивления; исключение здесь составляют только следующие случаи:
а) движение грунтовой воды, когда мы получаем ламинарный режим (см. гл. 17 и 18);
б) движение воды через модели сооружений (см. гл. 16);
в) редкие случаи русел большого поперечного сечения с весьма гладкими (например, стальными) стенками.
Учитывая сказанное, далее, как правило, будем иметь в виду только квадратичную область сопротивления. В настоящем параграфе применительно к этой области сопротивления рассмотрим напорное и безнапорное равномерные движения воды в цилиндрических руслах так называемого «правильного поперечного сечения» (см. начало § 4-2).
Отметим, что к «правильным руслам» относятся русла, имеющие поперечные сечения круглые, квадратные, прямоугольные, трапецеидальные, параболические и т. п. (при условии, что смоченная поверхность этих русел имеет однородную — одинаковую шероховатость). Такие сечения, как, например, звездообразные (встречающиеся в практике машиностроения), характеризующиеся наличием острых углов, мы здесь не будем рассматривать.
Имея в виду только равномерное движение (см. § 3-11), также исключим из рассмотрения движение воды на начальных участках цилиндрических русел (рис. 4-21), поскольку для этих участков эпюры скоростей в живых сечениях имеют особый вид, отличный от вида, свойственного равномерному потоку (следовательно, для этих участков и закон сопротивления движению воды будет иной).
1°. Формула Шези.Перепишем зависимость (4-69) в – виде
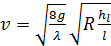 (4-94)
(4-94)
или в виде
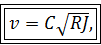 (4-95)
(4-95)
где v — средняя скорость в данном живом сечении; R — гидравлический радиус; J — пьезометрический уклон, равный в рассматриваемом случае равномерного движения гидравлическому уклону [см. (3-109) и (3-110)].
Формула (4-95) называется формулой Шези. Она имеет очень большое значение в практике. Коэффициент С (общепринятое обозначение), входящий в (4-95), называется коэффициентом Шези.
Сопоставляя (4-94) и (4-95), видим, что
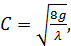 (4-96)
(4-96)
а следовательно,
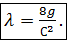 (4-97)
(4-97)
Формулы (4-96) и (4-97) связывают коэффициент гидравлического трения λ. и коэффициент Шези С. Как видно, зная λ, легко найти С. Поскольку λ является безразмерным коэффициентом, то коэффициент Шези, как видно из (4-96), имеет размерность. Размерность С равна корню квадратному из размерности ускорения.
Так как λ для квадратичной области сопротивлений зависит только от относительной шероховатости стенок русла и не зависит от числа Рейнольдса, а следовательно, и от рода жидкости, движущейся в русле, то в отношении С мы можем сказать то же самое: С зависит от относительной шероховатости стенок русла и не зависит от скорости движения v и вязкости жидкости, т. е. от коэффициента v (разумеется, если формулу Шези мы будем распространять и на область доквадратичного сопротивления, то в пределах этой области величина С окажется зависящей от Re).
В практике обычно величину С принято определять по специальным формулам (см. ниже § 4-13); вообще же говоря, значение С для случая круглых и прямоугольных труб можно находить и по формуле (4-96).
Надо учитывать, что формула Шези (4-95), строго говоря, может использоваться только для квадратичной области сопротивления в случае установившегося равномерного движения жидкости в руслах так называемого «правильного» поперечного сечения (см. выше).
2°. Зависимости, вытекающие из формулы Шези.Исходя из формулы (4-95), можно получить следующие практически важные расчетные зависимости:
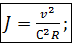 (4-98)
(4-98)
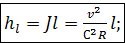 (4-99)
(4-99)
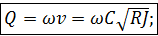 (4-100)
(4-100)
где l – длинна потока.
3°. Модуль расхода К. Введем обозначение
(I) 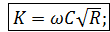 (4-101)
(4-101)
при этом формула (4-100) перепишется в виде
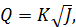 (4-102)
(4-102)
(II) 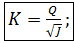 (4-103)
(4-103)
Как видно, модуль расхода К имеет два выражения: (I) и (II). Из (4-102) следует, что К представляет собой расход Q при J = 1,0. Из этой же формулы видно, что размерность величины К та же, что и расхода Q (поскольку J = hl: l — величина безразмерная).
Из формулы (4-103) получаем:
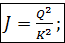 (4-104)
(4-104)
а следовательно,
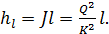 (4-105)
(4-105)
4°. Модуль скорости W. Введем обозначение
(I) 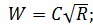 (4-106)
(4-106)
при этом формула (4-95) перепишется в виде
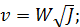 (4-107)
(4-107)
и, следовательно, для равномерного движения
(II) 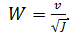 (4-108)
(4-108)
Как видно, модуль скорости W имеет два выражения: (I) и (II). Из (4-107) следует, что W представляет собой скорость v при J = 1,0. Размерность W та же, что и v.
Из (4-108) получаем:
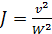 , (4-109)
, (4-109)
а следовательно,
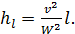 (4-110)
(4-110)
Понятиями модуля расхода К и модуля скорости W широко пользуются при практических расчетах труб и каналов.
5°. Эмпирические формулы для определения коэффициента Шези С.Решим уравнение Шези (4-95) в отношении С:
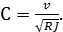 (4-111)
(4-111)
Наблюдая какой-либо водоток и замеряя в натуре величины v, R и J, можем по формуле (4-111)вычислить С для рассматриваемого водотока.
Многие исследователи проводили подобного рода измерения, и в результате было предложено много различных эмпирических формул для С. Эти формулы дают, конечно, разную величину С для данного конкретного случая. Такое положение объясняется приближенностью упомянутых эмпирических формул.
Таблица 4-3
Коэффициент шероховатости п для различных водотоков (для размеров в метрах и секундах)
| Материал стенок русла или описание водотока | Минимальный nmin | Нормальный n | Максимальный nмакс |
| А. Трубы и туннели | |||
| Стекло............................................................................ | 0,009 | 0,010 | 0,013 |
| Латунь............................................................................ | 0,009 | 0,010 | 0,013 |
| Сталь: | |||
| а) фланцевые и сварные соединения.............. | 0,010 | 0,012 | 0,014 |
| б) клепаные и резьбовые соединения............. | 0,013 | 0,016 | 0,017 |
| Чугун: | |||
| а) с покрытием битумом................................... | 0,010 | 0,013 | 0,014 |
| б) без покрытия битумом................................. | 0,011 | 0,015 | 0,016 |
| Деревянная клепка........................................................ | 0,010 | 0,012 | 0,014 |
| Деревянная обработанная обшивка............................ | 0,015 | 0,017 | 0,020 |
| Бетонная труба без засорения...................................... | 0,010 | 0,011 | 0,013 |
| Бетонная труба с некоторым засорением................... | 0,011 | 0,013 | 0,014 |
| Бетонная труба с необработанной поверхностью, выполняемая в гладкой деревянной опалубке | 0,012 | 0,014 | 0,016 |
| То же в негладкой опалубке........................................ | 0,015 | 0,017 | 0,020 |
| Дренажная труба (из обожженной глины) | 0,011 | 0,013 | 0,017 |
| Канализационная труба, покрытая осадками сточных вод.......................................................................... | 0.012 | 0,013 | 0.016 |
| Б. Облицовки безнапорных каналов | |||
| Асфальт.......................................................................... | 0,013 | — | 0,016 |
| Сталь неокрашенная..................................................... | 0.011 | 0,012 | 0,014 |
| Сталь окрашенная......................................................... | 0,012 | 0,013 | 0,017 |
| Дерево сгроганое.......................................................... | 0.010 | 0,012 | 0,014 |
| Цементный раствор...................................................... | 0,011 | 0,013 | 0,015 |
| Бетон затертый.............................................................. | 0,011 | 0,013 | 0,015 |
| Торкрет........................................................................... | 0,016 | 0,020 | 0,025 |
| Бетон по ровной скальной поверхности.................... | 0,017 | 0,020 | — |
| Бетон по неровной скальной поверхности................ | 0,022 | 0,027 | — |
| В. Безнапорные каналы без облицовки | |||
| В-1. Нескальный грунт | |||
| Чистый, только что выполненный............................. | 0,016 | 0,018 | 0,020 |
| Чистый, после выветривания...................................... | 0,018 | 0,022 | 0,025 |
| Чистый; ложе канала гравелистое.............................. | 0,022 | 0,025 | 0,030 |
| В канале небольшая растительность........................... | 0,022 | 0,027 | 0,033 |
| Заросший травой........................................................... | 0,025 | 0,030 | 0,033 |
| С густой травой и водорослями.................................. | 0,030 | 0,035 | 0,040 |
| Откопанный драглайном или землечерпалкой (без растительности)............................................................ | 0,025 | 0,028 | 0,033 |
| То же с растительностью.............................................. | 0,035 | 0,050 | 0,060 |
| Не поддерживаемый в исправности (трава и кусты не расчищаются)........................................................... | 0,050 | 0,100 | 0,140 |
| В-2. Скальный грунт | |||
| С гладкими стенками................................................... | 0,025 | 0,035 | 0,040 |
| С неровными стенками................................................ | 0,035 | 0,040 | 0,050 |
| Г. Естественные водотоки | |||
| Г-1. Малые потоки (шириной менее 30 м) | |||
| Равнинные..................................................................... | 0,025 | 0,070 | 0,150 |
| Горные........................................................................... | 0,030 | 0,045 | 0,070 |
| Г-2. Русла с поймой | |||
| Пойма без кустарников и деревьев............................. | 0,025 | - | 0,050 |
| Пойма, покрытая кустарником................................... | 0,035 | — | 0,160 |
| Пойма, покрытая деревьями........................................ | 0,110 | — | 0,200 |
| Г-3. Большие потоки | |||
| Правильные поперечные сечения русла; кустарников и валунов нет......................................................... | 0,025 | — | 0.060 |
Примечание. Значения п, обычно рекомендуемые для проектирования, набраны в таблице жирным шрифтом Эмпирические формулы для С, в которые входит и, были приведены в тексте книги для размеров в метрах и секундах.
Если, однако, отбросить устаревшие формулы для С и пользоваться более совершенными, то оказывается, что расхождение между величинами С, найденными по этим формулам для данного конкретного случая, не столь велико.
Приведем здесь только следующие формулы для С (размеры в метрах и секундах).
1. Так называемая сокращенная формула Гангилье — Куттера:
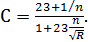 (4-112)
(4-112)
где n-коэффициент шероховатости стенок русла (имеющий размерность).
Гангилье и Куттер составили краткую таблицу численных значений n для стенок русла разной шероховатости. В табл. 4-3 приводим уточненные значения n, заимствованные из [4-9].
Таблици 4-4
Значения коэффициента С по формуле Маниинга 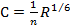 (метры и секунды)
(метры и секунды)
| R, м | п | ||||||||||
| 0,011 | 0,013 | 0,014 | 0,017 | 0,020 | 0,025 | 0,030 | 0,035 | 0,040 | 0,045 | 0,050 | |
| 0,30 | 74,4 | 63,0 | 58,4 | 48,1 | 40,9 | 32,7 | 27,3 | 23,4 | 20,4 | 18,2 | 16,4 |
| 0,32 | 75,2 | 63,6 | 59.1 | 48,6 | 41,4 | 33,1 | 27,5 | 23,6 | 20,7 | 18,4 | 16,5 |
| 0,34 | 76,0 | 64,3 | 59,7 | 49,1 | 41,8 | 33,4 | 27,8 | 23,9 | 20,9 | 18,6 | 16,7 |
| 0,36 | 76,7 | 64,9 | 60,3 | 49.6 | 42,2 | 33,7 | 28,1 | 24,1 | 21,1 | 18,7 | 16,9 |
| 0,38 | 77,4 | 65,5 | 60,8 | 50,1 | 42,6 | 34,0 | 28,4 | 24,3 | 21,3 | 18,9 | 17,0 |
| 0,40 | 78,1 | 66,0 | 61,3 | 50,5 | 42,9 | 34,3 | 28,6 | 24,5 | 21,4 | 19,1 | 17,2 |
| 0,42 | 78,7 | 66,6 | 61,8 | 50,9 | 43,3 | 34,6 | 28,9 | 24,7 | 21,6 | 19,2 | 17,3 |
| 0,44 | 79,3 | 67,1 | 62,3 | 51,3 | 43,6 | 34,9 | 29,1 | 24,9 | 21,8 | 19,4 | 17,4 |
| 0,46 | 79,9 | 67,6 | 62,8 | 51,7 | 43,9 | 35,2 | 29,3 | 25,1 | 22,0 | 19,5 | 17,6 |
| 0,48 | 80,4 | 68,1 | 63,2 | 52,0 | 44,2 | 35,4 | 29,5 | 25,3 | 22,1 | 19,7 | 17,7 |
| 0,50 | 81,0 | 68.5 | 63,6 | 52,4 | 44,5 | 35,6 | 29,7 | 25,5 | 22,3 | 19,8 | 17,8 |
| 0,55 | 82,3 | 69,6 | 64,6 | 53,3 | 45,3 | 36,2 | 30,2 | 25,9 | 22,6 | 20,1 | 18,1 |
| 0,60 | 83,5 | 70,6 | 65,6 | 54,0 | 45,9 | 36,7 | 30,6 | 26,2 | 23,0 | 20,4 | 18,4 |
| 0,65 | 84,6 | 71,6 | 66,5 | 54,7 | 46,5 | 37,2 | 31,0 | 26,6 | 23,3 | 20,7 | 18,6 |
| 0,70 | 85,7 | 72,5 | 67,3 | 55,4 | 47,1 | 37,7 | 31,4 | 26,9 | 23,6 | 20.9 | 18,8 |
| 0,75 | 86,7 | 73,3 | 68,1 | 56,1 | 47,7 | 38,1 | 31,8 | 27,2 | 23,8 | 21,2 | 19,1 |
| 0,80 | 87,6 | 74,1 | 68,8 | 56,8 | 48,2 | 38,5 | 32.1 | 27,5 | 24,1 | 21,4 | 19,3 |
| 0,85 | 88,5 | 74,9 | 69,5 | 57,2 | 48,7 | 38,9 | 32.4 | 27,8 | 24,3 | 21.6 | 19,5 |
| 0,90 | 89,3 | 75,6 | 70,2 | 57,8 | 49,1 | 39,3 | 32,8 | 28,1 | 24,6 | 21,8 | 19,7 |
| 0,95 | 90,1 | 76,3 | 70,8 | 58,3 | 49,6 | 39,7 | 33,0 | 28,3 | 24,8 | 22,0 | 19,8 |
| 1,00 | 90,9 | 77,0 | 71,4 | 58,8 | 50,0 | 40,0 | 33,3 | 28,6 | 25,0 | 22,2 | 19,9 |
| 1,10 | 92,4 | 78,2 | 72,6 | 59,8 | 50,8 | 40,6 | 33,9 | 29,0 | 25,4 | 22,6 | 20,3 |
| 1,20 | 93,7 | 79,3 | 73,6 | 60,6 | 51.5 | 41,2 | 34,4 | 29,5 | 25,8 | 22,9 | 20,6 |
| 1,30 | 95,0 | 80,4 | 74,6 | 61,5 | 52,2 | 41,8 | 34,8 | 29,8 | 26,1 | 23,2 | 20,9 |
| 1,40 | 96,2 | 81,4 | 75,6 | 62,2 | 52,9 | 42,3 | 35,3 | 30,2 | 26,4 | 23,5 | 21,2 |
| 1,50 | 97,3 | 82,3 | 76,4 | 62,9 | 53,5 | 42,8 | 35,7 | 30,6 | 26,8 | 23,8 | 21,4 |
| 1,60 | 98,3 | 83,2 | 77,2 | 63,6 | 54,1 | 43,3 | 36,1 | 30,9 | 27,0 | 24,0 | 21,6 |
| 1,70 | 99,3 | 84,1 | 78,0 | 64,3 | 54,6 | 43,7 | 36,4 | 31,2 | 27,3 | 24,3 | 21,9 |
| 1,80 | 100,3 | 84,8 | 78,8 | 64,9 | 55,1 | 44,1 | 36,8 | 31,5 | 27,6 | 24,5 | 22,1 |
| 1,90 | 101,2 | 85,6 | 79,5 | 65,5 | 55,6 | 44,5 | 37,1 | 31,8 | 27,8 | 24,7 | 22,3 |
| 2,00 | 102,0 | 86,3 | 80,2 | 66,0 | 56,1 | 44,9 | 37,4 | 32,1 | 28,1 | 24,9 | 22,5 |
| 2,20 | 103,7 | 87,7 | 81,5 | 67,1 | 57,0 | 45,6 | 38,0 | 32,6 | 28,5 | 25,3 | 22,8 |
| 2,40 | 105,2 | 89,0 | 82,7 | 68,1 | 57,8 | 46,3 | 38,6 | 33,1 | 28,9 | 25,7 | 23,2 |
| 2,60 | 106,6 | 90,2 | 83,8 | 69,0 | 58,6 | 46,9 | 39,1 | 33,5 | 29,3 | 26,1 | 23,5 |
| 2,80 | 108.0 | 91,3 | 84,8 | 69,8 | 59,4 | 47,5 | 39,6 | 33,9 | 29,7 | 26,4 | 23,7 |
| 3,00 | 109,2 | 92,4 | 85,8 | 70,6 | 60,0 | 48,0 | 40,0 | 34,3 | 30,0 | 26,7 | 24,0 |
| 3,50 | 112,0 | 94,8 | 88.0 | 72,5 | 61,6 | 49,3 | 41,1 | 35,2 | 30,8 | 27,4 | 24,6 |
| 4,00 | 114,5 | 97.0 | 90,0 | 74.1 | 63,0 | 50,4 | 42,0 | 36,0 | 31,5 | 28,0 | 25,2 |
| 4,50 | 116,8 | 98,8 | 91.8 | 75,6 | 64,2 | 51,4 | 42,8 | 36,7 | 32,1 | 28,6 | 25,7 |
| 5,00 | 118,9 | 100,6 | 93,4 | 76,9 | 65,4 | 52,3 | 43,6 | 37,4 | 32,7 | 29,1 | 26.1 |
2. Формула Маннинга:
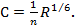 (4-113)
(4-113)
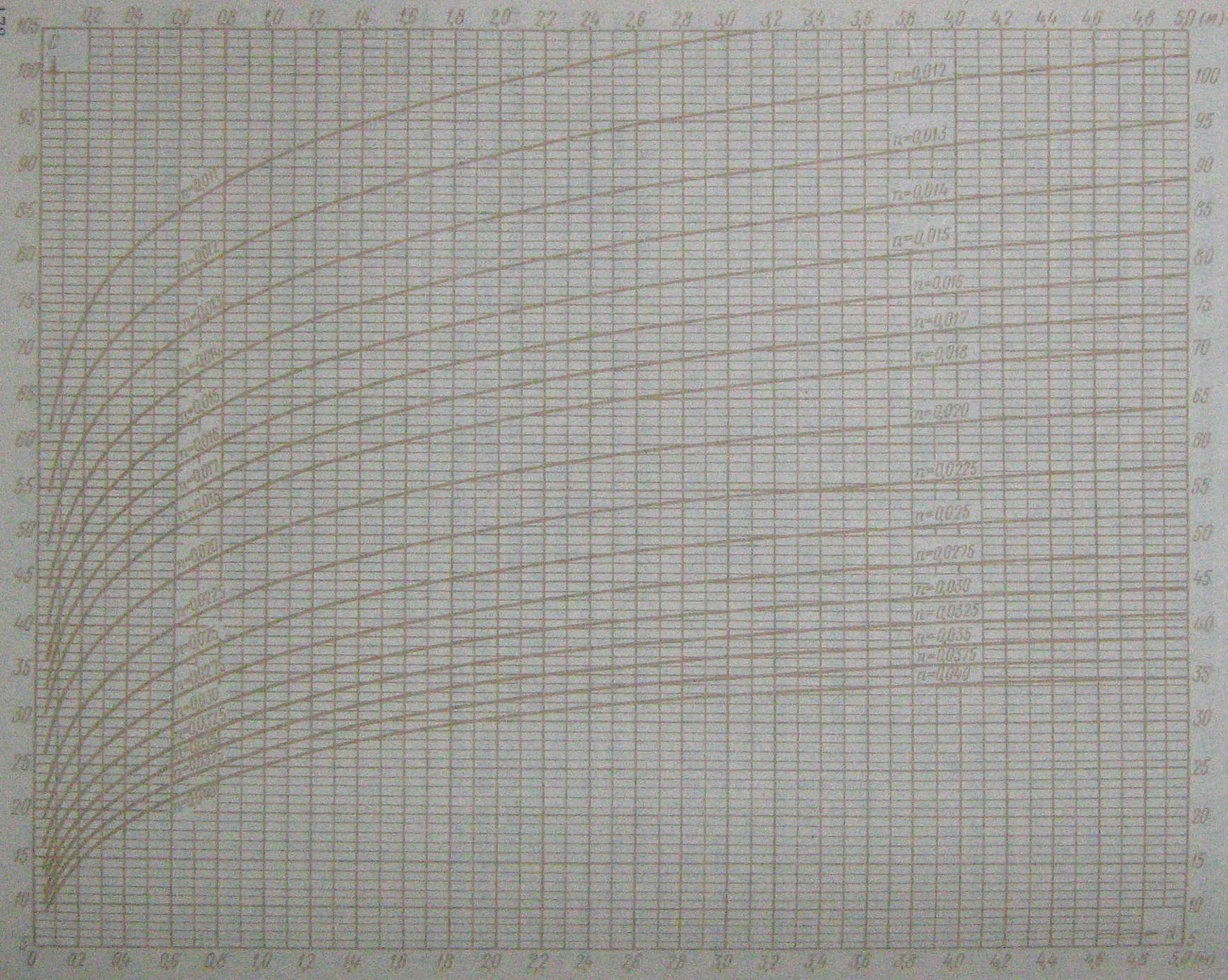
3. Формула Павловского, полученная для случая, когда R < (3,0 ÷ 5,0):
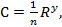 (4-114)
(4-114)
где
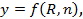 (4-115)
(4-115)
причем для у дается относительно сложная эмпирическая формула (здесь не приводимая).
4. Формула[30] Бахметева и Федорова:
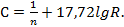 (4-116)
(4-116)
В формулы (4-113)— (4-116) входит коэффициент шероховатости, который назначается по шкале Гангилье и Куттера (табл. 4-3).
Практически вычислять С по этим формулам почти никогда не приходится, так как применительно к ним составлены соответствующие расчетные таблицы и графики. Например, применительно к формуле Павловского составлен график на рис. 4-26. Применительно к наиболее удобной формуле Маннинга — табл. 4-4. Установив по табл. 4-3 значение п, относящееся к данному конкретному случаю, и определив гидравлический радиус, мы по упомянутому графику или табл. 4-4 легко можем найти С. Надо подчеркнуть, что все приведенные эмпирические и полуэмпирические формулы для С (относящиеся к равномерному установившемуся движению жидкости) являются приближенными, причем значения и, входящие в них, приходится устанавливать по табл. 4-3 на основании чисто описательных (а не количественных) характеристик русла (так же как и значения Δ; см. выше). Поэтому при выборе для расчета той или другой из приведенных формул главным образом обращают внимание на простоту определения С по принятой формуле.[31] С этой точки зрения непосредственное применение в расчете формулы Павловского не может быть оправдано: эта формула, являясь весьма сложной, включает в себя, вместе с тем, весьма приближенный параметр п.
Как видно, в рассматриваемой области существует два разного вида оформления расчета: а) расчет с использованием величин Δ и λ и б) расчет с использованием коэффициента п. Заметим, что во всяком случае при расчете земляных каналов и естественных русел, должен использоваться второй вид расчета (с применением коэффициента п, в отношении которого мы имеем значительно более обширные экспериментальные данные, чем в отношении величины Δ).[32]
В литературе встречаются также формулы для С, относящиеся к области доквадратичного сопротивления. К числу таких формул принадлежит, например, так называемая полная формула Гангилье — Куттера; согласно этой формуле, которая имеет относительно сложный вид и рекомендуется ее авторами для применения в случае J < 0,005, величина С оказывается зависящей не только от R и п, но и от J.
А. Д. Альтшуль, используя некоторые полуэмпирические зависимости, предложил для открытых русел так называемую обобщенную формулу, действительную для квадратичной и для доквадратичной областей сопротивления, а также для области гладких русел:
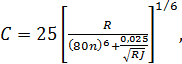 (4-117)
(4-117)
где R - в м; С - в м1/2/с
Эта зависимость при больших RJ (квадратичная область) оказывается аналогичной формуле Маннинга; при малых же RJ и малых значениях коэффициента п (гладкие русла) она дает результаты, близкие к тем, которые получаются по так называемой формуле Блазиуса. Значения коэффициента п, входящего в (4-117), можно брать из табл. 4-3.

Дата добавления: 2015-12-29; просмотров: 4470;
