СУЖЕНИЕ ТРУБОПРОВО. ВХОД В ТРУБОПРОВОД

На рис. 4-32 показаны различные случаи сужения трубопровода. Если предположить, что сечение «первой» трубы весьма велико, то вместо сужения трубопровода на рис. 4-32 получаем схемы входа потока из бассейна больших размеров в трубу.

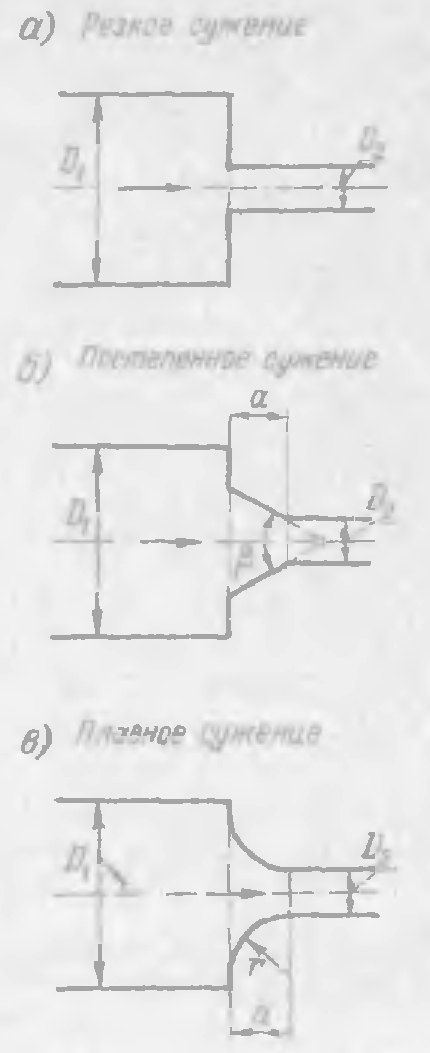
Рис. 4-32. График для определения коэффициента φ_у, входящего в формулу (4-140)

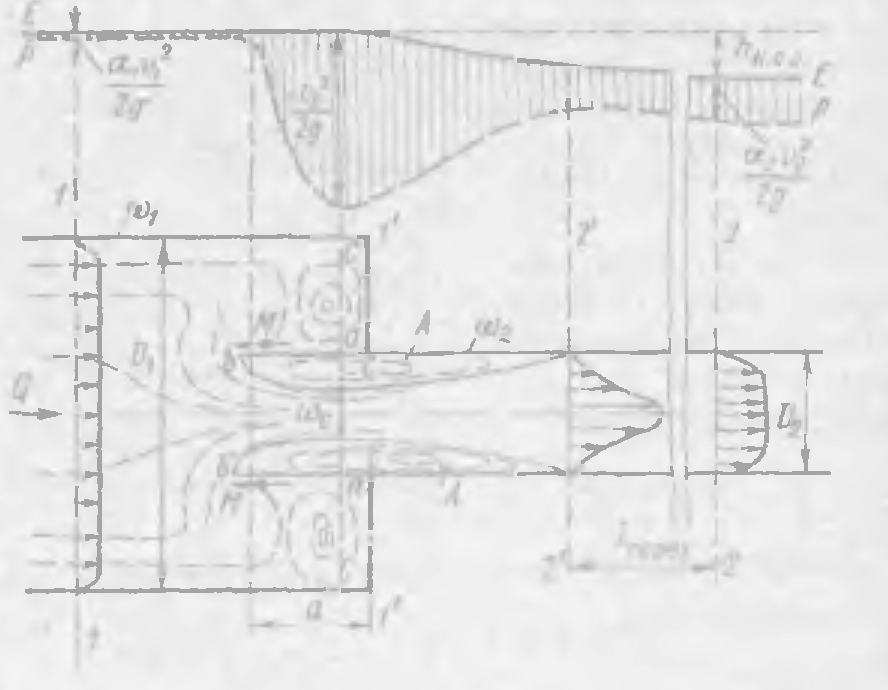
Рис. 4-33. Наиболее резкое сужение трубопровода

На рис. 4-33 представлен особый случай сужения, который может быть назван наиболее резким сужением. Если размер а (см. чертеж) удовлетворяет условию а > 0,5D₂, то этот случай в отличие от остальных может быть решен (с некоторым все же приближением) теоретически примерно так же, как резкое расширение трубы (см. § 4-15).

Рассмотрим случай наиболее резкого сужения. Условия протекания жидкости здесь характеризуются следующим (рис. 4-33):

1) частицы жидкости М, движущиеся вдоль стенки ab, должны в точках b резко изменить направление своего движения на противоположное. При этом благодаря силам инерции частиц струя оторвется от стенки bс и мы получим кольцевую водоворотную область А.

2) в пределах водоворотной области А можно различать два участка транзитной струи: сужающийся, расположенный перед «сжатым сечением» С— С, и расширяющийся, расположенный за сжатым сечением С — С.

Как показывают опыты, потеря напора на сужающейся части струи (до сечения С — С) для турбулентного потока относительно мала в связи с тем, что пульсация скоростей на протяжении сужающихся потоков всегда снижается; кроме того, и длина сужающейся части струи невелика — равна примерно 0,5 D₂.

В основном местная потеря напора сосредоточивается в пределах расширяющейся части струи (между сечениями С — С и 2' — 2').

Имея в виду такое положение, потерю напора для наиболее резкого сужения трубопровода (рис. 4-33) можем найти по формуле Борда, подставив в (4-129) вместо скорости v₁ скорость v_c в сжатом сечении С — С:

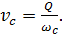(4-141)

где ω_с — площадь живого сечения транзитной струи в сжатом сечении
С — С:

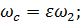(4-142)

здесь 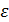называется коэффициент сжатия струи

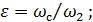(4-143)

Используя указанные зависимости, получаем величину потерь напора для наиболее резкого сужения (н. р. с.)

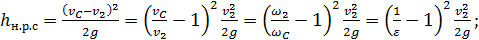(4-144)

или

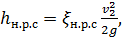(4-145)

где коэффициент сопротивления наиболее резкого сужения потока

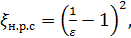(4-146)

Как видно, с уменьшением е, т. е с увеличением сжатия струи в сечении С—С, коэффициент сопротивления должен увеличиваться и, следова­тельно, должны увеличиваться потери напора. Если пренебречь потерями напора до сжатого сечения С — С, как мы делали выше, то следует считать, что полученные формулы (4-145) и (4-146) относятся, собственно, к любой схеме,изображенной на рис. 4-32. Различие между этими схемами будет заключаться только в разных численных значениях коэффициента ε, входящего в формулу (4-146).

Условимся обозначать далее коэффициент сжатия для «наиболее резкого 1 сжатия» (рис. 4-33) через 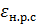. Величина этого коэффициента, согласно И. Е. Идельчику, оказывается[43]

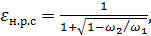(4-147)

Подставляя (4-147) в (4-148), получаем

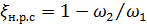(4-146)

Рассмотренное наиболее резкое сужение, характеризуемое соотношениями (4-147) и (4-148), является наиболее неблагоприятным: для него имеем самую большую местную потерю. Остальные случаи характеризуются меньшим сжатием струи в сечении С — С, а следовательно, и меньшими потерями напора

В общем случае (рис. 4-32) местную потерю напора h_c для сужающегося трубопровода определяют по формуле:

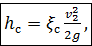(4-149)

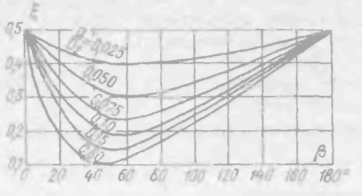
Рис. 4-34. График для определения «коэффициента ξ смягчения сужения», представленного на рис. 4-32, б

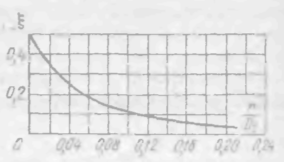
Рис. 4-35. График для определения «коэффициента ξ смягчения сужения», представленного на рис. 4-32, в

где коэффициент сопротивления сужения ξ _с трубопровода считают равным:

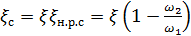, (4-150)

причем здесь ξ называют коэффициентом смягчения сужения.

Величину ξможно определить, пользуясь следующими эмпирическими данными.

1. Случай резкого сужения (р. с) трубопровода (рис. 4-32, a)

,

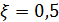а следовательно, коэффициент сопротивления, входящий в формулу (4-149) и обозначаемый здесь через ξ _р.с., оказывается

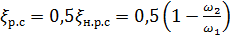. (4-151)

2. Случай постепенного сужения трубопровода (рис. 4-32,б). Здесь величина ξ находится в зависимости от угла β и отношения a/D₂ (см. чертеж) по графику на рис. 4-34. Как видно из этого графика, минимальная потеря напора на вход получается при β = 40 ÷ 60°.

3. Случай плавного сужения трубопровода (рис. 4-32,в). Здесь величину β

находим в зависимости от r/D₂ (где r — радиус скругления боковых стенок входа) по графику на рис. 4-35. Коэффициент ξ достигает минимума (ξ = 0,03) при r/D₂ = 0,2 и далее остается постоянным.

Экспериментальные графики на рис. 4-34 и 4-35, заимствованные из [4-5], даются здесь для случая круглоцилиндрических труб. Однако этими графиками можно пользоваться и при расчете прямоугольных труб; но тогда при определении по графикам коэффициента ξ, входящего в формулу (4-150), под величиной D₂ следует понимать гидравлический диаметр соответствующего водовода (D_r)₂ [см. зависимость (4-83)].

Рассмотрим в заключение случай входа в трубопровод из весьма большого бассейна. Для этого случая, полагая в формуле (4-150) площадь ω = ∞, получаем

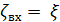. (4-152)

где 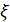, — можем найти, как указано выше.

Зная 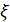_вх, потерю напора на вход h_вх определяем по формуле (4-149), заменив в ней обозначения h_c и 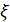_с обозначениями h_вх и 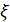_вх. Подчеркнем, что величина 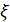_вх для случая входа в трубопровод, конструктивно оформленного в соответствии с рис. 4-32, а (т. е. для случая «резкое сужение») получается равной [при ω₁ = ∞; см. формулу (4-151)]

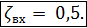(4-153)