ТРИ ВИДА УРАВНЕНИЯ БЕРНУЛЛИ

Представим на рис. 4-54 элементарную струйку и ее поперечное сечение 1—1. Обозначим через V объем жидкости, проходящий за некоторое время t₀ через сечение струйки 1—1. При этом вес этого объема G = γV, а масса М = ρV= 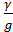V; механическую энергию жидкости, принадлежащую объему V, обозначим через Е_v.

Выше величину E_v мы относили к единице веса жидкости. Однако, вообще говоря, величину E_v можно относить также и к единице объема, и к единице массы движущейся жидкости. Слова «удельная величина» следует понимать здесь, как «относительная величина», т.е. величина, отнесенная к чему-либо (например, к объему жидкости или к весу этого объема или к массе этого объема).

В связи со сказанным, можно написать три разных выражения для удельной энергии движущейся жидкости (энергии, отнесенной к единице веса, к единице объема и к единице массы); эти выражения получают следующий вид (где L, t, P — символы соответственно длины, времени и силы):

1) мера энергии, принадлежащей единице веса движущейся жидкости

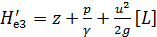(4-168)

достаточно Н'_е умножить на вес объема V и мы получим механическую энергию этого объема жидкости;

2) мера энергии единицы объема жидкости:

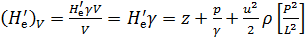(4-169)

3) мера энергии единицы массы жидкости

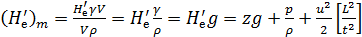(4-170)

достаточно (H'_е)_т умножить на массу объема V и мы получим механическую энергию этого объема. Можно написать:

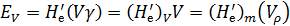(4-171)

где величины Н'_е, (H'_e)_v и (Н'_е)_т являются соответствующими напорами. В связи с наличием сил трения в реальной жидкости величина E_v по течению должна уменьшаться.

Перейдем к рассмотрению целого потока реальной жидкости, причем величину Q будем считать постоянной вдоль течения: Q = const.

Будем пользоваться понятием только двух напоров Н'_е и (Н'_е)_т [напора (Н'_е)_у касаться не будем]. При этом можем написать следующие три вида уравнения Бернулли, из которых каждый вид этого уравнения будет относиться к определенному случаю движения жидкости:

1-й вид: обший случай установившегося движения жидкости, когда жидкость является относительно тяжелой, т. е. [см. уравнение (4-170)] величиной (zg) нельзя пренебрегать сравнительно с величиной 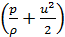. В этом случае получаем обычное уравнение Бернулли:

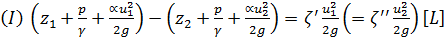(4-172)

где ζ - безразмерные «коэффициенты сопротивления»;

2-й вид: частный случай установившегося движения жидкости, когда жидкость является относительно легкой, т. е. когда величиной (zg) следует пренебречь сравнительно с величиной 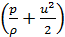. В этом случае, исходя из уравнения (4-170) получаем:

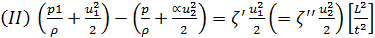(4-173)

можно сказать, что здесь мы пренебрегаем работой силы тяжести по сравнению с работой сил трения;

3-й вид: частный случай предыдущего вида движения, когда мы имеем равномерное движение, т. е. v₁= v₂ (жидкость легкая, причем v = const вдоль течения):

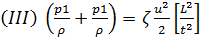(4-174)

Рассматривая полученные выше три вида уравнения Бернулли, подчеркнем следующие два важных обстоятельства:

1-е обстоятельство: легко показать, что при идентичных условиях безразмерные коэффициенты сопротивления 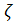, входящие в уравнения (4-173) и (4-174), численно равны соответствующим коэффициентам, входящим в уравнение (4-172).[50]

2-е обстоятельство: напор Н_е в отличне от напоров (Н_е)_V и (Н_е)_m имеет размерность длины. Поэтому очень важную геометрическую интерпретацию уравнения Бернулли удобно (физически доходчиво) проводить, пользуясь именно величиной напора Н'_е, а не {Н'е)_V или (Н'_е)m; кроме того, пользуясь величиной Н'_е, мы можем удобно использовать пьезометрические трубки и трубки Пито для выполнения соответствующих замеров.

Дополнительно из рассмотрения уравнений (4-172), (4-173) и (4-174) можно сделать следующие существенные выводы:

1) в случае «реальной» жидкости, обладающей достаточно большой величиной у (например, в случае воды) напор Н_е в нижерасположенном (по течению) живом сечении (сечении 2—2) всегда должен быть меньше, чем напор Н_е в вышерасположенном живом сечении (в сечении 1—1); при этом, как видно, движение «тяжелой» жидкости оказывается направленным в сторону меньшей величины Н_e, но не в сторону области, характеризуемой меньшим давлением р; в данном случае давление р во «втором сечении» может быть и меньшим и большим, чем в «первом сечении»;

2) в случае реальной жидкости, обладающей малым удельным весом (например, в случае движения воздуха), соответствующий напор в нижерасположенном (по течению) живом сечении (сечении 2 — 2) также должен быт меньшим, чем напор в вышерасположенном живом сечении (1 — 1), но давление р в сечении 2—2 может быть большим Можно утверждать, что движение «легкой» жидкости оказывается направленным в сторону области с меньшей величиной напора:

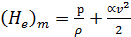(4-175)

а не в сторону области меньшего давления р;

3) только в случае равномерного движения «легкой» жидкости (например, равномерного движения воздуха) движение жидкости [см. зависимость (4-174)], оказывается направленным в сторону меньшего давления р.

Дополнительное замечание:

1) Рассмотрим невесомую жидкость. В этом случае в уравнении Бернулли следует полагать g = 0, а следовательно, и gz = 0. При этом приходится пользоваться понятием напора 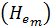как энергии, отнесенной к единице массы. Как видно, мы получаем |следующие выражения для такого напора (пренебрегая коэффициентом а):

а) в случае гидродинамик

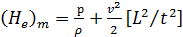(4-176)

б) в случае гидростатики:

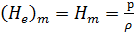(4-177)

Эти формулы выражают меру энергии, принадлежащей единице массы рассматриваемого объема невесомой жидкости.

2) Известно, что в случае конической расходящейся короткой трубы при истечении из нее «тяжелой жидкости» в атмосферу мы получаем напорную и пьезометрическую линии (линии ЕЕ и РР) в виде, изображенном на рис. 4-55, a (на этом рисунке изображены линии ЕЕ и РР для случая идеальной и для случая реальной тяжелой жидкости).

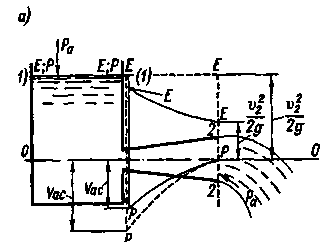
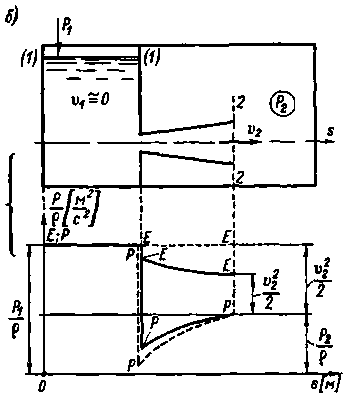
Рис 4-55. Истечение из расширяющейся конической трубы: а — «тяжелой» жидкости 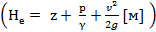; б — «легкой» (или невесомой) жидкости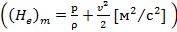

Е - E — напорная линия: Р — Р — пьезометрическая линия; -для идеальной жидкости; - для реальной жидкости

В случае легкой (или невесомой) жидкости изображать соответствующие линии ЕЕ и РР приходится уже не на той схеме, где изображена сама короткая труба, а на другом чертеже: на графике, где по вертикали откладываются величины, имеющие размерность не длины, а размерность 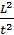; см. рис. 4-55, б. Этот чертеж (для идеальной и для реальной жидкости) строится в соответствии с уравнением (4-173).

[1] При турбулентном движении отмеченное условие обычно может быть удовлетворено, когда мы имеем однородную (одинаковую) шероховатость по всей длине смоченного периметра русла

[2] Точнее говоря, возникающая на поверхности соприкасания жидких слоев друг с другом.

[3] Коэффициент вязкости обозначают иногда не буквой η, а буквой μ.

[4] Здесь можно поступить и иначе: вместо того, чтобы вводить в формулу (4-22) абсолютное значение 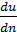, можем условиться всегда проводить нормаль n от поверхности S в сторону возрастающих скоростей.

[5] Пользуясь так называемым обобщенным законом Ньютона (здесь не приводимым), можно показать, что зависимость (4-24) выражает также и касательные напряжения для площадок, взятых в плоскости живых сечений. Из механики твердого тела известно, что касательные напряжения, действующие по двум взаимно перпендикулярным площадкам, должны быть равны между собой по величине.

[6] Наличие такой (нулевой) скорости на стенке (даже абсолютно гладкой) можно, по-видимому, в какой-то мере объяснить, используя модель «твердой воды» (см. конец § 1-4).

[7] Зависимость (4-26) написана в предположении, что величина 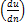во всех точках поверхности S₀ одинакова. В противном случае имеем:. .

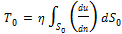[8] Схема водоворотов а, b, с на чертеже показана упрощенной. Можно представить себе вращение жидкости и по схеме более сложной (см., например, водоворот d).

[9] Индекс «а» у скорости u_а — первая буква слова «актуальная».

[10] Принятые направления Ах и Az не обязательно горизонтальны или вертикальны. Строго говоря, скорость и_а следовало бы разлагать не на два, а на три направления и оперировать тремя проекциями: (и_а)_x, (и_а)_z и (и_а)_у. Мы же для простоты пояснения рассматриваем как бы плоскую задачу (что в действительности не имеет места).

[11] Далее, как правило, горизонтальных черточек над буквой и, а также р, ставить не будем.

[12] На рис. 4-13, а для примера показан случай интенсивной турбулентности, когда в некоторые моменты времени актуальные скорости оказываются направленными даже в сторону, противоположную общему движению.

[13] Предполагается, что площади эпюр №1 и №2 должны быть равны.

[14] Замену поперечных скоростей u_z касательными напряжениями иногда поясняют на следующем примере. Представим себе, что по реке движутся рядом (в данный момент времени), но с разными скоростями два судна, нагруженные камнями. Положим, что камни с судна, идущего с меньшей скоростью, перебрасываются на судно, идущее с большой скоростью, и наоборот: камни с судна, движущегося с большей скоростью, перебрасываются на судно, идущее с меньшей скоростью. Ясно, что в результате такой переброски камней судно, идущее с большей скоростью (получив некоторое количество камней, обладающих небольшими поступательными скоростями, равными скорости судна, идущего с малой скоростью) будет, в связи с инерцией переброшенных камней, замедлять свой -ход; судно же, идущее с меньшей скоростью — ускорять свой ход.

Ясно также, что тот же самый эффект мы можем получить не перебрасывая камни с одного судна на другое, а введя между бортами двух рассмотренных судов силу трения (являющуюся парной) определенной величины; такое воображаемое трение будет способствовать замедлению быстро идущего судна и ускорению медленно идущего судна

[15] Чтобы определить необходимую величину τ_т, используют как бы постулат, который условно можно представить такой записью:

[16] Вывод этой формулы приведен петитом [4-11].

[17] Далее вертикальные черточки у 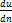опускаем, считая, что ось n всегда направлена

в сторону увеличивающихся скоростей u.

[18] Иногда динамический коэффициент турбулентной вязкости обозначается буквой А.

[19] При этом обтекание выступов шероховатости происходит с отрывом струи от них (см далее § 4-14).

[20] Эта степенная формула является несколько менее точной, чем формулы, дающие логарифмический закон распределения скоростей. Зависимость типа (4-64) применялась

и ранее, как чисто эмпирическая (с постоянным коэффициентом m) для расчета скоростей в реках.

[21] В другой форме подобная зависимость еще ранее предлагалась Г. В. Железняковым для квадратичной области сопротивления — для течения воды в реках (безиспользования коэффициента λ).

[22] Ниже будем рассматривать только верхнюю поверхность пластинки.

[23] Небольшой площадью ΔΩ этой эпюры, обусловленной некоторой перестройкой набегающего потока (диктуемой уравнением неразрывности), пренебрегаем.

[24] В этой области реальная жидкость движется как твердое тело (см. рис. 3-4, а).

[25] При достаточно равномерном распределении τ₀ по смоченному периметру

[26] График, показанный на рис. 4-25, опытным путем был Получен также рядом других авторов: Муди (в 1944 г.), Г. А. Муриным (в 1948 г.) и др.

[27] Эти данные в сокращенном виде заимствованы из книги [4-4].

[28] По этому вопросу см. дополнительно статью Н. А. Картвелишвили, Сборник научно-методических статей по гидравлике. Вып. 3. — М.: Высшая школа, 1979.

[29] Ниже «черту осреднения» над величинами Δ и 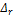не ставим.

[30] Экспериментальную проверку этой формулы выполнил И. И. Агроскин [4-11, с. 145].

[31] Для различных теоретических исследований наиболее удобной является формула Маннинга степенного типа.

[32] В [4-9 и 4-10] приводятся фотографии различных русел с указанием рекомендуемых для них численных значений п. Эти фотографии в некоторой мере могут облегчить выбор величины п для данного конкретного случая.

[33] Вывод этого выражения для Ф, исходя из обычных «гидравлических представлений», приводится в статье В. Н. Цепилова «Функция диссипации механической энергии для решения обычных задач гидравлики (о работе сил внутреннего трения в жидкости)». Сборник научно-методических статей по гидравлике. Вып. № 5. — М.: Высшая школа, 1982.

[34] Часто эти области называют «вихревыми». Такое название неудачно, так как в пределах транзитной струи движение жидкости является также вихревым (см. § 3-4). Иногда области А называют «мертвыми зонами», что также нельзя признать удачным.

[35] Иногда участок длиной (l′_в + l_в′′)называют участком дестабилизации потока, а участок длиной l_перех — участком стабилизации потока

[36] См. рис. 8-1. При определенных условиях в районе сечения 2 — 2 у дна русла, как показывают опыты, возникает водоворотная зона (не представленная на рис. 8-1).

[37] Этого объяснения отрыва транзитной струи, даваемого нами, в литературе мы не

находим.

[38] На рис. 4-29, а показан частный случай — симметричное растекание потока.

[39] При рассмотрении наклонной трубы окончательные результаты получаются те же, что и для горизонтальной трубы.

[40]

[41] На рис. 4-30,6 и в представлена картина осредненного потока, симметричная относительно продольной оси трубопровода. В действительности, однако, в подобных случаях почти всегда получается искривление оси транзитной струи, причем водоворотные области оказываются несимметричными; часто может получиться отрыв струи только от мной стенки.

[42] Как нам представляется, достаточно надежно количественно решить вопрос об отрыве транзитной струи тяжелой реальной жидкости от стенки русла едва ли можно (в общем случае) без учета отмеченного нами «энергетического принципа». Дополнительно обратим внимание на то, что на рис. 4-30, г (и на рис. 4-29, а) имеется в виду случай, когда боковой приток энергии h_ΔE пристенной струйке, принадлежащей водоворотной области, меньше потерь энергии в этой струйке. Следует учитывать, что при отсутствии h_ΔE водоворотные области (см., например, рис. 4-29, a) существовать не могут. Только наличие h_ΔE обусловливает возможность возникновения и существования этих областей.

[43] Вывод формулы (4-147) см., например, [11, с. 157]

[44] Большинство этих данных взяты по книге [4-5].

[45] При рассмотрении тройников мы пользуемся термином «снижение напора» вместо термина «потеря напора» (см. § 4-19).

[46] В литературе приводится ряд предложений, уточняющих формулу (4-159'). При этом большинство авторов отмечает, что формула Киршмера дает заниженную величину потерь, напора. Иногда считают, что в правую часть этой формулы надо вводить поправочный множитель, равный 1,75 ÷ 2,00.

[47] См. Б. А. Дергаче в. Случаи увеличения полного напора по течению реальной I жидкости (для «целого потока» при установившемся движении). Сборник научно-методических статей по гидравлике. Вып. 3.—М.: Высшая школа, 1980.

[48] См. предыдущую сноску.

[49] Как видно, величины напоров для разных точек вертикального живого сечения откладываются от линии aе по горизонтали.

[50] Для доказательства справедливости этого положения достаточно: а) умножить на величину g обе части уравнения (4-172) и б) затем положить (z₁g — z₂g) = 0.