ПОВОРОТ ПОТОКА. СОЕДИНЕНИЕ И РАЗДЕЛЕНИЕ ПОТОКОВ

1°. Условия протекания жидкости в пределах поворота трубы. На повороте трубы получаем искривление линий тока (рис. 4-36,6). На частицы жидкости, движущиеся по искривленным линиям тока, действует центробежная сила инерции. За счет этой силы гидродинамическое давление (а следовательно, и потенциальная энергия) в месте поворота у внешней стенки трубы повышается, а у внутренней — понижается. Это же обстоятельство обусловливает уменьшение скоростного напора (удельной кинетической энергии) у внешней стенки и увеличивает его у внутренней стенки. Таким образом, на повороте происходит перераспределение скоростей по живым сечениям и деформация эпюр скоростей вдоль потока (как показано на рис. 4-36, б)

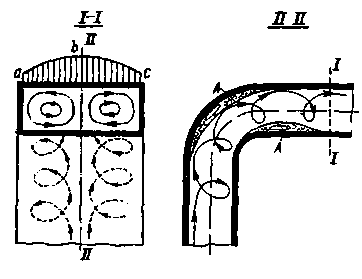
Рис. 4-51. Течение на повороте трубы

На рис. 4-36, б показан отрыв транзитной струи в двух местах. Надо заметить, что отрыв струи от внутренней стенки увеличивается за счет инерции частиц жидкости, движущихся вдоль этой стенки (в пристенном слое по пути от сечения 1—1 до точки с).

При плавном повороте трубы указанные отрывы струи могут отсутствовать. В этом случае местные потери напора в значительной мере обусловливаются имеющимся на повороте «парным вихрем» (винтовым движением, вызванным действием сил инерции). Такое винтовое движение, характеризуемое наличием так называемой поперечной циркуляции (иначе «вторичными течениями»), показано на рис. 4-51, где для примера изображена прямоугольная труба. На этом чертеже показана эпюра давления на стенку трубы, ограниченная кривой abc. Как видно, в центральной части внешней стенки трубы давление оказывается наибольшим (в связи с большими скоростями и в этой части трубы). Такое положение и обусловливает движение жидких частиц влево и вправо (вдоль внешней стенки) от центральной части к периферии.

2°. Соединение потоков (рис. 4-52).[47] В этом случае получаем «поверхность раздела» а — б. Благодаря турбулентному перемешиванию «ступенчатая» эпюра скоростей, получающаяся в сечении АВ (эта эпюра на рисунке не показана), выравнивается на длине l и приобретает в сечении 2 — 2 «нормальный» вид. Через поверхность раздела а — б (в связи со сказанным в § 3-16) должна передаваться удельная энергия ΔЕ. Между сечениями 1—1 и 2—2 могут возникать отрывы струи от стенки русла, в связи с чем будут появляться водоворотные области.

Наличие сил трения в жидкости обусловливает: а) неравномерное распределение скоростей в сечениях 1, 2 и 3; б) передачу энергии жидкости через поверхность раздела а — б (от 1-го потока к 3-му или наоборот от 3-го потока к 1-му потоку); в) диссипацию энергии, а следовательно, уменьшение энергии по течению. Для простоты пояснения пренебрежем этими обстоятельствами (обстоятельствами а, б, в), причем условно будем считать, что в пределах рассматриваемого небольшого участка потока (между сечениями 1 — 1, 2 — 2, 3—3) жидкость является идеальной.

Принимая такое допущение, можем в соответствии с законом сохранения энергии написать следующее энергетическое уравнение

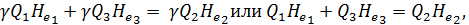(4-161)

где Q₁, Q₂ и Q₃ — расходы жидкости для отдельных труб (см. рисунок); 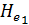, 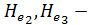напоры (полные удельные энергии) соответственно в сечениях 1, 2 и 3.

Из уравнения (4-161), учитывая, что

Q₁+Q₃ = Q₂ (4-162)

легко получить зависимость (для идеальной жидкости на пути от сечения 1 — 1 до сечения 2—2):

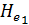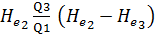= (4-163)

Из рассмотрения этой зависимости видно следующее:

1) При Q₃ = 0, т. е. при отсутствии присоединения расхода, в случае идеальной жидкости 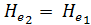,, , что и должно быть согласно уравнению Бернулли.

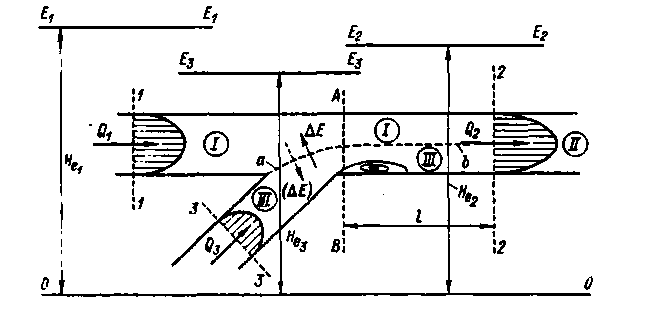
Рис. 4-52. Схема соединения двух потоков

2) Если Q₃ ≠ 0, т. е. если мы имеем по длине потока переменный расход (Q ≠ const), то для идеальной жидкости получим 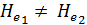причем могут иметь место случаи, когда оказывается, что 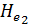> 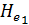т. е. напор (полная удельная энергия) по течению идеальной жидкости увеличивается.

Отмеченные положения (см. пп. 1 и 2) вытекают из рассмотрения закона сохранения энергии. Здесь необходимо помнить, что уравнение Бернулли (3-101) справедливо только для частного случая, когда по длине потока расход Q является постоянным (Q = const).

Если бы мы рассматривали в данном узле не идеальную жидкость, а реальную, то в принципиальном отношении у нас ничего бы не изменилось (имели бы место только количественные, но не качественные изменения).

В случае идеальной, а также реальной жидкости, напорные линии Е— Е в рассматриваемом узле потока могут располагаться, как показано на рис. 4-52; как видно, переходя от потока III к потоку II, мы можем получить для реальной жидкости увеличение полноте напора по течению ( > ).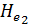

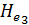3°. Разделение потоков.[48] Чтобы разъяснить отмеченный выше «парадокс», рассмотрим разделение потока (рис. 4-53).

Построим для сечения 1 — 1 (см. на рисунке живое сечение abcde) эпюру напоров 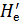(относящихся к элементарным струйкам, составляющим рассматриваемый поток):

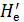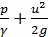= z + , (4-164)

где (z + ) = const для данного живого сечения а—е.

Такая эпюра выражается на рисунке площадью a-b-c-d-e-a.[49] Осредняя ординаты этой эпюры в пределах всего живого сечения 1—1 потока, получаем напор 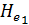[см. 1 зависимость (3-100)]:

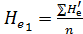, (4-165)

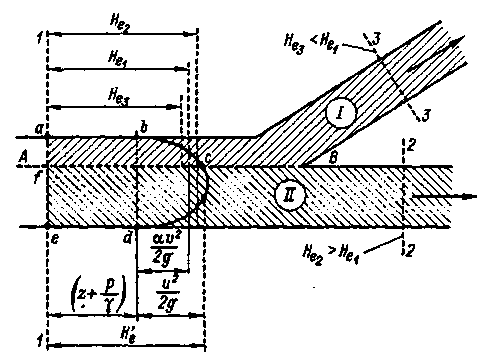
Рис. 4-53. Схема разделения потока на две(I и II части)

Эпюры напоров 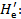1-(abcfa) – для сечения af; 2 – (fcdef)-для сечения ef; 3-(abcdea)- для всего живоо сечения ae

Выделим теперь на рис. 4-53 линией АВ две части рассматриваемого потока I к II (эти части на рисунке покрыты штриховкой разного наклона): При этом можем отметить следующее:

а) эпюра напоров Н'е для I части / потока выражается площадью abcfa; осредняя напоры Н'е в пределах части af живого сечения, получаем напор Не₃ (см. рисунок), меньший чем Не₁:

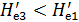(4-166)

б) эпюра напоров Н'_е для I части II потока выражается площадью fcdef; осредняя напоры Н'_e в пределах части fе живого сечения, получаем напор Н_е2 больший чем напор Н_е1 :

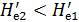(4-167)

Таким образом полный напор для целого потока реальной жидкости может изменяться по течению не только в связи с «потерей напора» (обусловленной работой сил трения), но также еще и в связи с отделением (или присоединением) на пути от сечения 1 — 1 и до сечения 2 —2 соответствующих масс жидкости.

В связи со сказанным, рассматривая выше местные потери напора в тройниках (стр. 195), мы различаем «коэффициент потерь напора» («коэффициент сопротивления») и «коэффициент изменения напора».