ОБЩИЙ ХАРАКТЕР МЕСТНЫХ ПОТЕРЬ НАПОРА

1°. Два вида явления отрыва транзитной струи от стенок русла. При

обтекании турбулентным потоком какой-либо преграды (рис. 4-28, а) происходит отрыв транзитной струи от стенки русла. При этом получаем области А, заполненные множеством водоворотов; такое водоворотное движение в этих областях носит резко выраженный неустановившийся характер. Будем именовать: области А водоворотными (или, иначе, вальцовыми или циркуляционными) областями;[34] остальную часть потока — транзитной струей; поверхность abcd, отделяющую транзитную струю от водоворотных зон,— поверхностью раздела.

Поверхность раздела бывает выражена нерезко; она носит неустановившийся и неустойчивый характер: периодически эта поверхность получает местные искривления, которые прогрессируют и переходят в отдельные водовороты (вальцы); эти водовороты попадают затем в транзитную струю и уносятся ею; поверхность же раздела снова восстанавливается с тем, чтобы в последующие моменты времени опять распасться и свернуться в водовороты, и т. д Постоянное возникновение в районе поверхности раздела водоворотов, попадающих в транзитную струю, способствует повышению пульсации скоростей и давлений в ней.

Переходя от рис. 4-28,а к осредненному потоку, водоворотные области показывают несколько условно — в виде, изображенном на рис. 4-28,б; штриховыми линиями здесь представлены линии тока осредненного потока, а не траектории частиц жидкости.

Именно в таком виде и будем изображать водоворотные области. Предполагается, что линия тока abсd на рис. 4-28, б намечена так, что: а) в любой ее точке осредненная (во времени) величина проекции актуальной скорости на нормаль к линии abсd равна нулю; б) величина расхода вдоль транзитной струи, выражаемая площадью соответствующей части эпюры скоростей, является постоянной. Строго говоря, такие условия могут быть удовлетворены только приближенно (если живые сечения считать плоскими).

Водоворотные области характеризуются возвратным течением. Эпюры осредненных скоростей дают нулевые значения продольных скоростей и не только на стенках русла, но и на «средней» линии водоворотной области (см. чертеж).

Сечение 2 — 2, где заканчивается вторая водоворотная зона, характеризуется как повышенной пульсацией скоростей и давлений, так и наличием сильно деформированной эпюры осредненных скоростей. На протяжении некоторого участка потока между сечениями 2 — 2 и 3—3 происходит: а) затухание пульсаций до величин, свойственных равномерному движению, и б) выравнивание эпюры скоростей, причем в сечении 3 — 3 эта эпюра принимает «нормальную» форму, свойственную равномерному течению.

Как видно, водоворотные области, расположенные между сечениями 1—1 и 2 — 2 (рис. 4-28, б), нарушают «нормальный» характер движения жидкости на некоторой длине l_перех от сечения 2 — 2 до сечения 3 — 3; этот участок назовем переходным или послеводоворотным.[35]

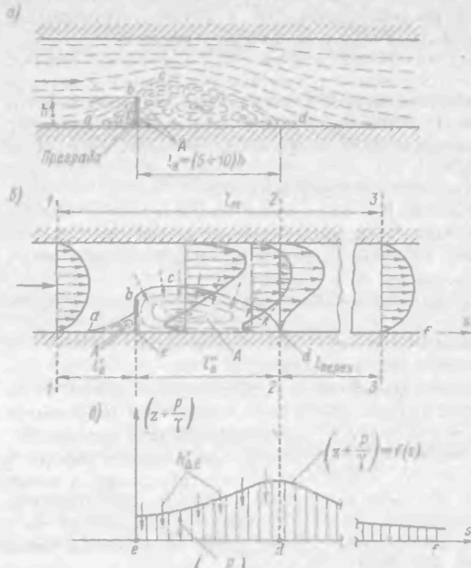
Рис. 4-28. Обтекание преграды турбулентным потоком:

а - действительный поток, б – осредненный поток (неполная воображаемая модель Рейнольдса — Буссинеска); поперечными стрелками показан поток энергии, поступающий в водоворотную зону со стороны транзитной струи; в — схема изменения величины (z + р/γ) вдоль стенки ef (у которой всюду u= 0)

Через поверхность раздела благодаря пульсационным поперечным скоростям происходит некоторый обмен жидкости между водоворотной областью и транзитной струей. Турбулентные касательные напряжения (см. § 4-7), действующие вдоль поверхности раздела, относительно велики. Поэтому потеря напора в пределах водоворотной зоны получается большая. На длине пе-реходного (послеводоворотного) участка имеем также повышенные потери напора сравнительно с дальнейшими участками равномерного движения.

Если по поверхности раздела bcd установить криволинейную твердую стенку русла, то получим безотрывную транзитную струю; потеря напора при этом значительно уменьшится. Такое снижение потерь напора объясняется тем, что касательные напряжения, возникающие вдоль установленной стенки, значительно меньше турбулентных касательных напряжений, действующих вдоль поверхности раздела.

Поясненный выше отрыв транзитной струи может быть назван (несколько условно) «инерционным отрывом транзитной струи от стенки русла». Помимо такого отрыва струи, можно различать еще «отрыв транзитной струи (а в соответствующих случаях и отрыв пограничного слоя), обусловленный диффузией механической энергии поперек потока». Примером отрыва струи, вызванного поперечной диффузией механической энергии, может являться поток в сильно расширяющемся насадке (см. рис. 4-30), а также случай так называемого гидравлического прыжка.[36] Такого рода отрывы, по нашему мнению, обусловливаются тем, что хотя полная удельная механическая энергия жидкости «целого потока» снижается по течению (за счет потерь напора), вместе с тем за счет поперечной диффузии энергии (направленной в сторону стенки русла; см. § 3-16) энергия, принадлежащая пристенной (придонной) элементарной струйке, начинает при определенных условиях увеличиваться по направлению общего (главного) течения жидкости (см. рис. 4-30,г).[37]

Такое положение, очевидно, позволяет объяснять более полно возможность возвратного течения тяжелой реальной жидкости в районе водоворотных областей, вызванных и «инерционным отрывом».

2°. Общий характер местных потерь напора. На отдельных участках русла (трубопровода), где имеются повороты, местные расширения и сужения русла и т. п., возникают местные потери напора, обусловленные, так же как и потери по длине, работой сил трения. Но эти силы трения в узлах резко изменяющегося движения, свойственных «местным сопротивлениям», распределяются в потоке весьма неравномерно.

Такие места потока в общем случае характеризуются:

а) местными искривлениями линий тока и живых сечений;

б) уменьшением или увеличением живых сечений вдоль потока;

в) возникновением местных отрывов транзитной струи от стенок русла,

а следовательно, появлением водоворотных областей.

В пределах такого рода узлов, а также в пределах некоторого расстояния за ними наблюдаем:

1) деформацию эпюр осредненных скоростей вдоль потока;

2) повышение пульсации скоростей и давлений.

Как было указано, повышение пульсации скоростей обусловливает увели-чение касательных турбулентных напряжений (в рассматриваемом осредненном потоке), что, в свою очередь, влечет за собой повышение потерь напора.

Таковы условия возникновения так называемых местных потерь напора h_j.

Рассматривая далее вопрос о величине местных потерь напора в случае турбулентного движения, будем иметь в виду только область квадратичного сопротивления.

В заключение подчеркнем, что местная потеря напора h_j в рассматриваемом выше частном случае (см. рис. 4-28) возникает на длине

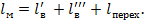
Напомним, (см. § 4-1), что длина l_м в практике часто бывает пренебрежимо малой сравнительно с общей длиной потока (трубопровода). Именно поэтому, как было выше отмечено, считают при выполнении обычных расчетов, что l_м = 0, причем найденное значение местной потери напора h_j относят к одному поперечному сечению потока; потерю же по длине h_l условно считают распределенной по всей длине рассчитываемого потока равномерно.

§ 4-15. ПОТЕРИ НАПOPA ПРИ РЕЗКОМ РАСШИРЕНИИ НАПОРНОГО ТРУБОПРОВОДА (ФОРМУЛА БОРДА). ВЫХОД ИЗ ТУРБУЛЕНТНОГО БАССЕЙНА.

На рис. 4-29, а показан случай, когда труба, имеющая диаметр D₁ переходит в трубу, имеющую больший диаметр D₂ (D₂ > D₁). Струя, выходящая из первой трубы, на некоторой длине l_В (в связи с наличием продольных сил трения, действующих на боковой ее поверхности) расширяется и в сечении 2' — 2' заполняет все сечение второй трубы. На длине l_В струи имеет место отрыв ее от стенок трубы и образование описанной выше водоворотной зоны А, имеющей в данном случае кольцевую форму. Струя в пределах между сечениями 1 — 1 и 2' — 2' может иметь несимметричный вид (получается искривление оси потока).[38]

На протяжении расширяющейся струи (между сечениями 1—1 и 2' — 2') и переходного участка (между сечениями 2' — 2' и 2—2) получаем неравномерное движение, местами резко изменяющееся.

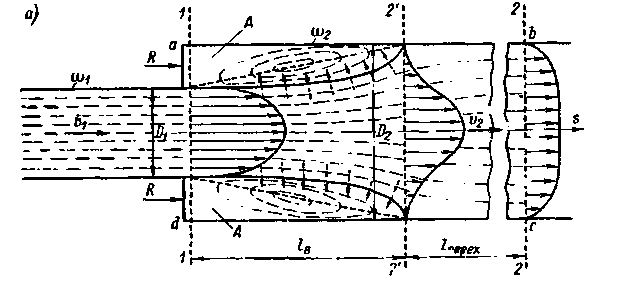
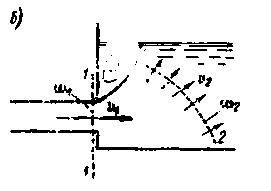
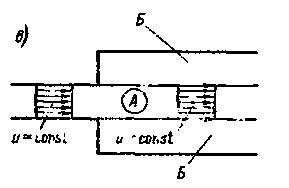
Рис. 4-29. Резкое расширение потока: а — к выводу формулы Борда; модель Рейнольдса—Буссинеска (поперечными стрелками показан поток энергии, передающийся от транзитной струи в водоворотную область); б — потери напора «на выход»; в — случай идеальной жидкости (А — цилиндрическая струя; Б — область покоящейся жидкости)

Между сечениями 1—1 и 2—2 возникает местная потеря напора h_j Эту потерю назовем потерей напора на резкое расширение (р. р) потока и далее будем обозначать ее через (h_j)_{p р} или просто через h_{p. р}. Впервые расчетную зависимость для h_{p p} получил французский инженер Борда, который уподобил резкое расширение струи явлению удара неупругих твердых тел. Заметим, что в связи с этим потерю h_{p p} иногда называют потерей на удар (что в настоящее время не следует делать).

Выведем формулу Борда, пользуясь гидравлическим уравнением кинетической энергии (уравнением Бернулли) и гидравлическим уравнением количества движения (рассматривая эти два уравнения как систему уравнений). Напомним, что уравнение Бернулли (полученное нами, исходя из теоремы, касающейся изменения кинетической энергии; см. начало § 3-12) учитывает как внешние, так и внутренние силы; гидравлическое же уравнение количества движения (см. § 3-22) учитывает только внешние силы. Решая совместно два эти уравнения, получаем возможность выделить работу внутренних сил трения, обусловливающих искомую потерю напора.

Имея в виду сказанное, соединяем сечения 1 — 1 и 2—2 уравнением Бернулли. В результате получаем

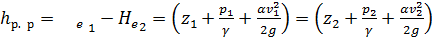(4-118)

Индексы 1 и 2 указывают, что соответствующие величины относятся или к сечению 1-1, или 2-2, где сечение 1-1 совпадает с линией 1-1.

Для упрощения рассуждений будем рассматривать только горизонтальную трубу.[39] В районе сечений 1 —1 и 2 — 2 имеем равномерное движение и потому корректив кинетической энергии а для этих сечений будем считать равным единице. При этом (4-118) перепишем в виде

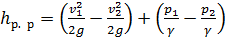(4-119)

Разность давлений (p₁ — p₂) найдем, пользуясь гидравлическим уравнением количества движения (3-124), которое приложим к отсеку жидкости abcd,соединив этим уравнением сечения 1 — 1 и 2 — 2:

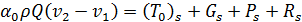(4-120)

где 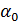— корректив количества движения, который для сечений 1 — 1 и 2 — 2 можно принять также равным единице; (T₀)_s — проекция на направление движения внешней силы трения Т₀, действующей со стороны стенок трубы на рассматриваемый отсек жидкости abcd. Так как длина участка потока между сечениями 1 — 1 и 2 — 2 невелика, то силой Т₀ пренебрегаем и считаем (T_o)_s = 0 (1-е допущение); G_s — проекция собственного веса отсека abcd на направление движения, G_s = 0; Р_s, — сумма проекций на ось s сил гидродинамического давления Р₁ и Р₂, действующих соответственно на торцовые сечения 1 — 1 и 2 — 2 выделенного отсека транзитной струи (со стороны жидкости, находящейся слева и справа от этого отсека); R_s — проекция (на направление движения) реакции стенок (без учета сил трения); величина R_s = R, где сила R — давление вертикальной стенки ad, имеющей кольцевую форму, на жидкость (см. чертеж).

Величину (Р_s, + R_s) можно представить в виде

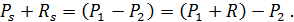(4-121)

Давление в сечении 2—2 распределяется по гидростатическому закону, поскольку здесь имеем равномерное движение. Примем, что давление по всему сечению 1 — 1 (по площади ad, охватывающей транзитную струю и водоворотную область) распределяется также по гидростатическому закону (2-е допущение). При этом можем написать:

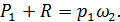(4-122)

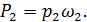(4-123)

где р₁ и р₂ — гидродинамические давления в центрах тяжести сечений 1 — 1 (круга ad) и 2 — 2 (круга be); ω2 — площадь сечения второй трубы (т. е. площадь круга ad или be). Подставляя (4-122) и (4-123) в (4-121), находим:

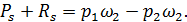(4-124)

Учитывая (4-124), уравнение (4-120) переписываем в виде

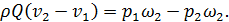(4-125)

откуда имея в виду, что

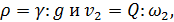(4-126)

получаем

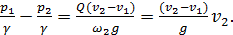(4-127)

Подставляя (4-127) в (4-119), имеем

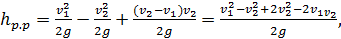(4-128)

или окончательно

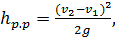(4-129)

где разность (v₁ — v₂) называют потерянной скоростью.

Формула (4-129) называется формулой Борда. Согласно этой формуле

потеря напора при резком расширении равняется скоростному напору, отвечающему потерянной скорости.[40]

1) Преобразование формулы Борда:

а) Приведем выражение (4-129) к другому виду. Вынесем за скобки v₁ тогда получим:

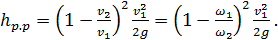(4-130)

Обозначая

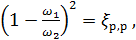(4-131)

имеем

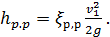(4-132)

б) Вынося за скобки v₂, получаем аналогично

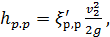(4-133)

где

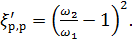(4-134)

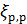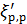Коэффициенты и называются коэффициентами сопротивления при резком расширении потока.

2) Местная потеря напора, получающаяся при выходе потока из трубы в бассейн больших размеров. Эту потерю называют потерей «на выход» (рис. 4-29,6), ее обозначают через h_вых.

Данный случай является частным случаем предыдущего, когда ω₂ значительно больше ω₁ (ω₂ >> ω₁). Имея это в виду, можем написать в соответствии с формулой (4-131), что

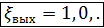(4-135)

а следовательно, потеря на выход будет

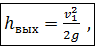(4-136)

или, несколько точнее

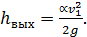(4-137)

Если ω₂ нельзя считать достаточно большой величиной, то h_выхможно представить зависимостью:

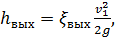(4-138)

где

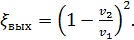(4-138)

В заключение отметим следующее.

1) Соединяя уравнением Бернулли и уравнением количества движения сечения 2' — 2' и 2 — 2, мы можем получить приближенную формулу для потерь напора на длине переходного участка, а затем и на длине «водоворотного участка» [4-11, с. 153].

2) Возникает вопрос о возможности распространения формулы Борда на случай ламинарного движения жидкости. Здесь надо сказать следующее. Если 2-е допущение (о гидростатическом распределении давления по сечению 1-1; см. рис. 4-29,а) приемлемо для турбулентного движения, то для ламинарного движения, когда водоворотная зона А может отсутствовать, указанное допущение без соответствующих коррективов является, как правило, неприемлемым.

3) Надо учитывать, что в случае идеальной (невязкой) жидкости, когда касательные напряжения τ вовсе отсутствуют, мы, естественно, не можем представить себе поток, показанный на рис. 4-29, а. При отсутствии τ продольные скорости и должны распределяться равномерно по живым сечениям (рис. 4-29, в). При этом жидкость во второй трубе (см. область Б), окружающая цилиндрическую струю А, должна находиться в покое.

Струю идеальной жидкости можно представить себе расширяющейся только при особых условиях (начальных и граничных).

§4-16. ПОСТЕПЕННОЕ РАСШИРЕНИЕ ТРУБОПРОВОДА
(ДИФФУЗОР)

Диффузор (рис. 4-30) устраивают для уменьшения потери напора h_p._p, возникающей при переходе трубы меньшего диаметра в трубу большего диаметра. Как показывает опыт, картина протекания жидкости в диффузоре имеет вид:

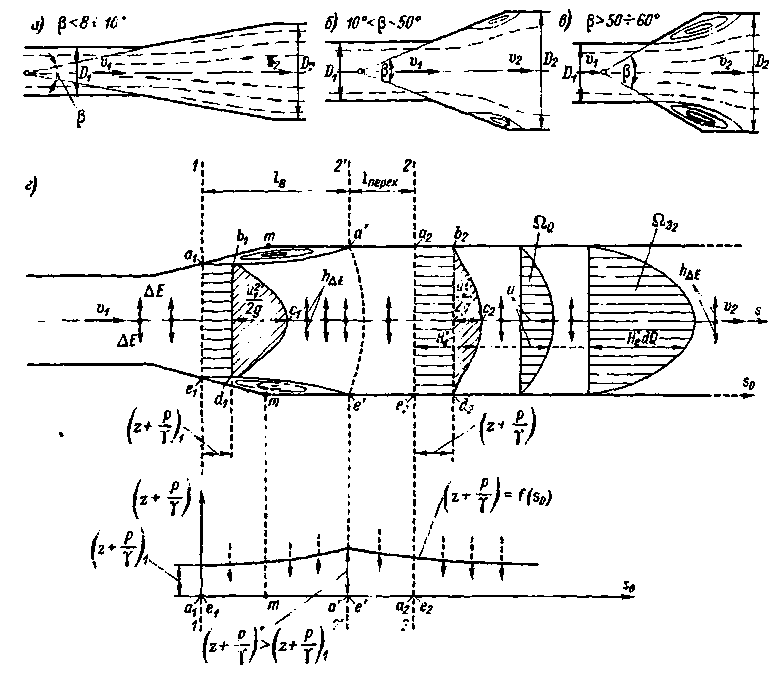
Рис. 4-30. Диффузоры (потоки представлены моделью Рейнольдса-Буссинеска); а) безотрывное движение; б) небольшой водоворот; в) сильно развитый водоворот; г) случай плоской задачи:

s₀ - координата, направленная по стенке трубы; abcdea - эпюры напора Н'_е; напор Н_е = (Ω_э): (Ω₀),где Ω₀- площадь эпюры скоростей (выражающая расход Q); Ω_э - площадь эпюры величины (H′edQ) [согласно формуле 3-95)]: а' - e' - неплоское живое сечение; l_перех - длина переходного участка

а) при угле β в пределах

0 < β < 8 ÷ 10°

на всем протяжении диффузора наблюдается безотрывное протекание жидкости (рис. 4-30, а);

б) при

8 ÷ 10° < β < 50 ÷ 60°

получается отрыв струи от стенок (рис. 4-30,6), причем с увеличением угла β точка начала отрыва перемешается вверх по течению;

в) при

β > 50 ÷ 60°

на всем протяжении диффузора имеем отрыв транзитной струи от стенок (рис. 4-30, в)[41]

Потерю напора в диффузоре h_дифф выражают в долях потери напора h_{p р,} вычисленной по формуле (4-129):

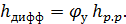(4-140)

где 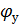- эмпирический коэффициент.

Величина φ_у в основном зависит от угла р. Как видно из графика (рис. 4-31), построенного на основании опытных данных, наивыгоднейший угол β, при котором получаются наименьшие потерн напора, будет β ≈ 6°.

В заключение отметим, что на рис. 4-30, г представлена схема (в виде модели Рейнольдса — Буссинеска), объясняющая (более подробно, чем то было сказано ранее) физические причины отрыва транзитной струи от стенки русла.

На этой схеме для, плоских живых сечений 1-1 и 2 - 2 изображены эпюры напоров Н'_е (для элементарных струек):

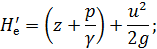
см. площади Q_a1b1c1d1e1a1 и Q_a2b2c2d2e2a2.

Площадь таких эпюр не выражает механическую энергию, проносимую жидкостью через живые сечения 1 - 1 и 2 - 2. Рассматривая для примера сечение 2 - 2, можем сказать, в соответствии с формулой (3-95), что энергию, проносимую через это сечение, выражает (для плоской задачи) площадь эпюры (Ω_э)₂, каждая горизонтальная ордината которой равна H'_edQ. Легко видеть, что полный напор в сечении 2—2 равен:

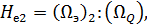
де 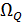- площадь эпюры скоростей, дающая нам (для плоской задачи) величину расхода Q (который вдоль потока постоянен: Q = const).

Площадь эпюры ( ), в связи с потерями напора, должна уменьшаться по течению также как и величина Н_е.

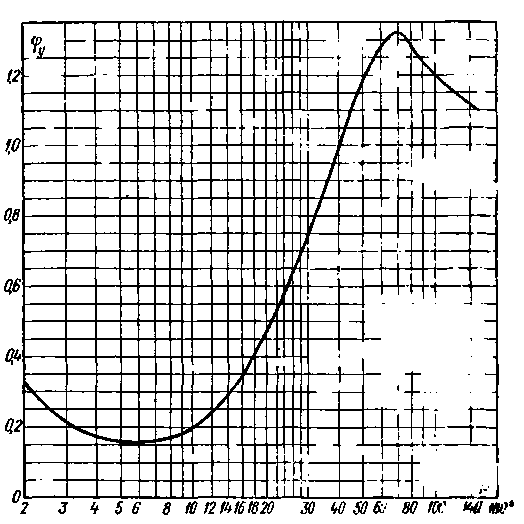
Рис. 4-31. График для определения коэффициента φ_у, входящего в формулу (4-140)

Вместе с тем, в связи с поперечной диффузией энергии полный напор у стенки трубы (где и ≈ 0) 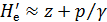[см. на рис. 4-30, г схему графика
(z + р/γ) = f (s₀)] может увеличиваться вдоль общего направления течения; такое положение, как мы отмечали ранее, и может обусловливать «возв­ратное» течение жидкости, а следовательно, и отрыв транзитной струи от стенки. В связи с отрывом струи возникает водоворотная зона, существование которой обеспечивается поперечной (по отношению к потоку жидкости) диффузией механической энергии.[42]