Диафрагма с острыми краями в трубе круглого поперечного сечения при

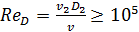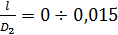и при (рис. 4-37):

,

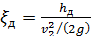где v₂ — средняя скорость в круглом отверстии диафрагмы площадью ω₂. Величина ζ_д берется из табл. 4-5 в зависимости от отношений ω₂/ω₁, и ω₂/ω₃ (обозначения ω₁ и ω₃ см. на чертеже).

2°. Резкий поворот трубы иа угол θ; рис. 4-38, а:

,

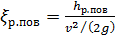где величина коэффициента сопротивления резкого поворота 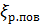для гладких труб круглого и квадратного поперечного сечения вычисляется по формуле

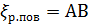, (4-156)

причем здесь эмпирические коэффициенты А и В берутся (согласно И. Е. Идельчику) из табл. 4-6 и 4-7.

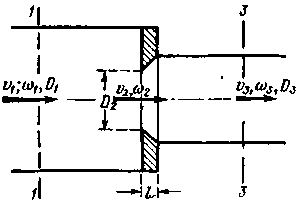
Рис. 4-37. Диафрагма

3°. Плавный поворот трубы на угол θ(при ReD≥2∙10⁵); рис. 4-38,б:

,

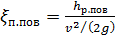где величина коэффициента сопротивления плавного поворота 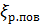для гладкой цилиндрической грубы вычисляется по формуле

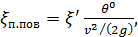(4-157)

причем здесь 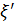берется из табл. 4-8, составленной по данным Вейсбаха.

4°. Тройник вытяжной (рис. 4-39); ω₁ = ω₂. Коэффициенты сопротивления ζ_2-3 и ζ′_2-3. учитывающие снижение[45] (изменение) напора (h)_2-3 от сечения 2 - 2 до сечения 3-3;

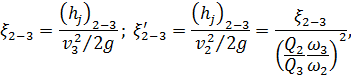
где 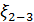находится по табл. 4-9 в зависимости от отношений ω₂/ω₃ и Q₂/Q₃ (обозначения указаны на чертеже)

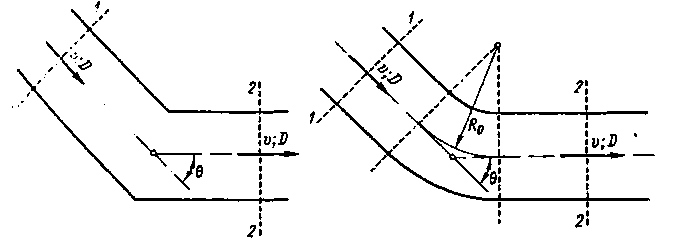
Рис. 4-38. Поворот трубы

Коэффициенты сопротивления 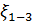и 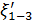, учитывающие снижение напора 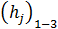от сечения 1 -1 до сечения 3 — 3 (рис. 4-39)

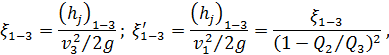
где 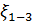находится по табл. 4-10 в зависимости от отношения .

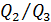Таблица 4-5