Анализ уравнения Кирхгоффа

Теплоемкость. Уравнение Кирхгоффа.

Тепловые эффекты процессов зависят от температуры, и эта зависимость определяется температурной зависимостью теплоемкости участвующих в реакциях веществ

Теплоемкость

Средней теплоемкостью вещества называется количество теплоты, поглощаемой или отдаваемой при нагревании или охлаждении одного моля или одного килограмма этого вещества на один кельвин:

С_ср =Q/ΔT (3.5)

Если речь идет об одном моле вещества, то теплоемкость мольная (молярная), если об одном килограмме, то – удельная. Соответственно, размерность теплоемкости – Дж/(мольК), Дж/(кгК).

Истинной теплоемкостью вещества называется предел, к которому стремится средняя теплоемкость при ΔТ→0:

C = lim (Q/ΔT) = δQ/dT (3.6)

ΔT→0

Здесь δQ/dT не является производной, поскольку δQ – это бесконечно малое количества теплоты, а не изменение свойства. Запишем последнее выражение так:

δQ= СdT (3.7)

и проинтегрируем его:

T₂

Q = ∫CdT (3.8)

T₁

Подставив уравнение (3.8) в (3.5) получаем уравнение, связывающее среднюю в интервале температур теплоемкость с истинной:

T₂

C_ср = (1/ΔT) ∫CdT (3.9)

T₁

Величина теплоемкости зависит от того, в каком процессе система получает или отдает теплоту Q. Практически наиболее важны процессы при постоянном давлении или постоянном объеме. Им отвечают, соответственно, изобарная и изохорная теплоемкости:

С_v = 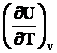С_p =

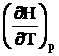
Связь С_р и С_v легко определяется для идеального газа:

dH= dU + pdV = dU + p R/p *dT = dU + RdT

(V = RT/p dV = R/p dT)

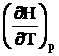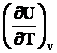= + R Þ C_p = C_V + R (3.10)

R – работа расширения, которую совершает 1 моль идеального газа при нагревании на 1^о

В рамках термодинамики теоретически вычислить величину теплоемкости не представляется возможным, поскольку она определяется характеристиками молекул и атомов, которые не анализируются термодинамикой, а рассматриваются в других разделах физической химии и в физике.

Очевидно, что для теоретического определения теплоемкости необходимо знать, как внутренняя энергия вещества меняется с температурой. Строго эта задача на сегодняшний день не решена, и теплоемкость определяют с той или иной степенью точности в разных интервалах температур. Наиболее просто – для идеального газа. В этом случае при средних температурах достаточно учесть энергию поступательного и вращательного движения молекул, которые не взаимодействуют между собой.

Согласно закону Дж. Максвелла, эта энергия равномерно распределяется по степеням свободы. Под степенями свободы понимают независимые движения частицы. Так, атом одноатомного газа имеет три степени свободы, поскольку может совершать поступательное движение в направлениях трех ортогональных осей декартовой системы координат. Каждая молекула двухатомного газа имеет дополнительно две вращательные степени свободы вокруг взаимно-перпендикулярных осей, то есть всего пять. Энергия вращения вокруг третьей оси, проходящей через центры атомов, мала, и ею можно пренебречь (рисунок 5). Для трехатомных молекул надо учитывать все три вращательные степени свободы, а всего их (вместе с поступательными) – шесть.

Поступательная энергия молекул практически не квантуется, т.е. может изменяться непрерывно. Когда системе сообщается тепло, то энергия передается через хаотические соударения молекул. При столкновениях молекулы обмениваются квантами энергии, величина которых зависит от температуры – «тепловыми квантами» – kT, где k – постоянная Больцмана

k = R/N = 1,38*10^-23Дж/К. (3.11)

При обычной температуре величина теплового кванта достаточна, чтобы изменить энергию поступательного и вращательного движения, а также наиболее слабых колебаний, но возбуждения сильных колебений, и тем более электронов не происходит

De_v>> kT > De_r (4.4)

Эта диаграмма позволяет примерно оценить теплоемкость простейших веществ.

Одноатомный газ (He, Ar)

Молекулы одноатомного газа как точечные массы совершают только поступательное движение и имеют три степени свободы. По принципу равномерного распределения энергии по степеням свободы можно определить энергию молекул. На одну степень свободы приходится в среднем e = 1/2kT, а для 1-го моля Е = 1/2RT. Cледовательно, на 3 степени свободы одноатомной молекулы приходится

U = 3/2 RT. (4.5)

С_v= 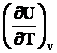= 3/2 R ~ 3 кал/моль*K = 12,5 Дж/мольК,

C_p = C_V + R = 5 кал/мольК

Теплоемкость одноатомных газов практически не зависит от температуры.

Двухатомный газ – линейная молекула

Каждая молекула имеет 3N степеней свободы, где N –число атомов в молекуле. Для двухатомной молекулы общее число степеней свободы равно 6, из них 3 поступательных, 2 вращательных и 1 колебательная. Вращательных степеней свободы у линейных молекул только 2, так как при вращении вокруг линии связи, молекула не изменяет своего положения и это движение не может изменяться за счет передачи энергии от другой молекулы. При комнатной температуре возбуждаются только поступательное и вращательное движение – 5 степеней свободы

U = 5/2 RT.

С_v = 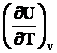= 5/2 R ~ 5 кал/мольK = 20,8 дЖ/мольК,

C_p = C_V + R = 7 кал/мольК,

При повышении температуры начинает постепенно возбуждаться колебательное движение, С_v→ 6 кал/(моль К).

Многоатомные молекулы.

Общее число степеней свободы равно 3N, из них 3 поступательных, 3 ( или 2 для линейных молекул) вращательных и 3N - 6 (5) колебательных. Колебания тоже могут быть разными: валентные (жесткие) колебания, в которых происходит изменение длины связи, требуют большой энергии для возбуждения, и деформационные, в которых изменяются углы между связями. Последние более мягкие и требуют меньших квантов для возбуждения, и, следовательно, могут возбуждаться при более низкой температуре. В общем можно сделать такой вывод: чем сложнее молекула, тем сильнее зависимость ее теплоемкости от температуры. Нельзя получить общей теоретической формулы, выражающей эту зависимость.

Если экспериментальные данные о теплоемкости веществ отсутствуют, обычно используют следующие правила:

- правило Дюлонга-Пти: теплоемкость твердых соединений приблизительно равна сумме атомных теплоемкостей, принимая , что для простых веществ они одинаковы и равны приблизительно 3R.

- правило Неймана-Коппа (правило аддитивности): теплоемкость сложного вещества равна сумме теплоемкостей образующих соединение простых веществ.

- мольные теплоемкости органических жидкостей рассчитывают суммированием атомно-групповых составляющих (инкрементов) теплоемкостей, значение которых являются табличными данными.

Так как теоретических общих уравнений для зависимости теплоемкости от температуры нельзя вывести, то используются экспериментальные зависимости в виде степенного ряда

для органических веществ С_р = а + bТ + сТ² + dT³; (4.9)

для неорганических веществ С_р = а + bТ + с' Т^-2. (4.10)

Уравнение Кирхгоффа – зависимость теплоты реакции от температуры

Большинство термохимических данных в справочниках приведено при температуре 298 К. Для расчета стандартных тепловых эффектов при других температурах используют уравнение Кирхгофа в дифференциальной форме:

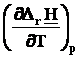= D_rС_p.

D_rС_p. = Dа + DbT + DcT² + Dd T³ + Dc'T^-2.

Анализ уравнения Кирхгоффа

1. D_rС_р = 0 D_rН_T1= D_rН_T2 . Теплота реакции не зависит от температуры.

2. DС_р>0, T­ D_rН ­ Для эндотермической реакции D_rН₂ > D_rН₁.

Для экзотермической реакции ½D_rН₂½ <½D_rН₁½.

3. DС_р < 0, T­ D_rН ¯ Для эндотермической реакции D_rН₂ < D_rН₁.

Для экзотермической реакции ½D_rН₂½ >½D_rН₁½.