Гидравлический расчет трубопроводов. Трубопрововоды подразделяются на простые и сложные

Трубопрововоды подразделяются на простые и сложные. Простые тру-бопроводы представляют собой последовательно соединенные участки с неизменным объемным расходом жидкости. К сложным относятся трубо-проводы с параллельно соединенными участками, с отбором жидкости по тракту, кольцевые трубопроводы, разветвленные сети.

Типичными задачами при расчете простых трубопроводовявляются:

– определение перепада давления, обеспечивающего заданную пропускную способность трубопровода, если известны длины и диаметры отдельных участков и тип местных сопротивлений;

– определение пропускной способности трубопровода при заданном перепаде давлений;

– определение диаметра трубопровода или отдельного участка, если известны перепад давления или пропускная способность.

Во всех случаях основным расчетным соотношением является

.

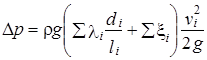При решении первой задачи по объемному расходу Q и диаметру di опре-деляют скорость жидкости

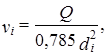
число Рейнольдса

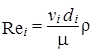
и коэффициент сопротивления по длине li, соответствующий этому числу Рейнольдса и относительной шероховатости участка (рис.34). Коэффициенты местных сопротивлений выбирают по справочным данным.

Остальные задачи решают методом последовательных приближений с уточнением на каждом шаге значений скорости и коэффициентов сопротивления по длине. Первое приближение можно подобрать графо-аналитически (рис.35).

Δ р Q Δp

Δ p2 Q2 Δp1

Δ pз Qз Δpз

Рис.35

Когда задан диаметр трубопровода, для нескольких значений пропускной способности рассчитывают потери давления по соотношению

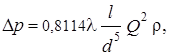
принимая значение коэффициента сопротивления по длине равным λ=0,03, по полученным данным в кординатах Δр-Q проводят параболу через начало координат и снимают значение пропускной способности как показано стрел-ками.

Это же уравнение используется для нахождения диаметра трубопровода по перепаду давления или пропускной способности.

Задачей расчета сложного трубопровода с параллельно включенными линиями (рис.36) является определение расходов жидкости в каждой линии и потерь напора по известному общему расходу.

Рис.36

Одинаковые во всех линиях потери напора равны

.

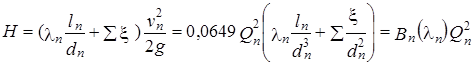Так как система, состоящая из n уравнений, содержит n+1 неизвестное, то ее необходимо дополнить балансовым уравнением

.

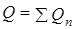В связи с тем, что коэффициенты сопротивления по длине в линиях зависят от расхода, эту задачу, как и две предыдущих, приходится решать методом последовательных приближений.