Потери напора по длине
Эти потери обусловлены наличием сил трения в потоке реальной жид-кости и, как было установлено еще Галилеем, зависят от скорости движения и плотности среды. Позже было установлено, что на них также влияет коэффициент динамической вязкости жидкости.
Указанные параметры вместе с определяющим размером канала образуют безразмерный комплекс, называемый числом или критерием Рейнольдса, значение которого определяет режим движения жидкости.
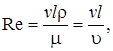
Существование принципиально различных режимов движения – лами-нарного и турбулентного – было обнаружено в опытах Хагена, Менделеева и самого Рейнольдса. Для первого из них характерна организованная структура потока, состоящего из неперемешивающихся струек. Во втором случае дви-жение частиц жидкости носит хаотический характер, вызывающий пере-мешивание потока.
Переход турбулентного режима в ламинарный происходит при определенной скорости, называемой критической. Ей соответствует число Рейнольдса Re= 2320. Переход же ламинарного режима в турбулентный происходит постепенно. Началу установившегося турбулентного режима течения соответствует значение Re= 13000.
Ламинарный режим
В установившемся параллельноструйном потоке выделим центральную элементарную струйку с радиусом r (рис.32) и c использованием закона Ньютона для силы внутреннего трения составим баланс сил, действующих на нее в горизонтальном направлении
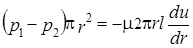 .
.
Отсюда
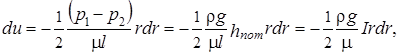
где I=hпот/l – пьезометрический уклон.





 |











 |




 R
R
r



L
Рис.32
Если пренебречь изменением давления по высоте канала, то I=Const, и интегрирование даст
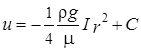 .
.
Константу интегрирования находим из граничного условия r=R, u=0. Окончательно имеем
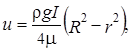
т.е. эпюра локальных скоростей потока представляет собой параболоид вращения.
Максимальная скорость достигается в центре трубы
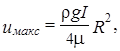
а средняя скорость потока равна
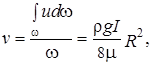 (15)
(15)
т.е. она в два раза меньше максимальной.
Из выражения (15) пьезометрический уклон составляет
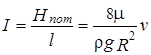
и потери напора по длине равны
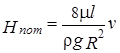 .
.
Как видно, они пропорциональны скорости движения жидкости. Эта закономерность была обнаружена Пуазейлем еще в 1840 г. опытным путем.
Несложные преобразования последнего выражения дают соотношение, называемое формулой Дарси-Вейсбаха
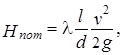
где l = 64/Re – так называемый коэффициент сопротивления по длине.
Можно показать, что в ламинарном режиме движения жидкости коэффициент Кориолиса равен α = 2.
Турбулентный режим
В неупорядоченном турбулентном потоке жидкости скорость в каждой точке непрерывно меняется по направлению и величине. Экспериментально, однако, установлено, что осредненная местная скорость, за исключением пристенного слоя, вследствие интенсивного перемешивания масс жидкости распределяется по поперечному сечению более равномерно, чем в ламинарном режиме (рис.33).
 |  |







Рис.33
Потери напора в турбулентном режиме по-прежнему определяют по формуле Дарси-Вейсбаха, но коэффициент сопротивления по длине в общем случае зависит не только от числа Рейнольдса, но и от шероховатости стенок труб. На шероховатость в свою очередь влияют материал, способ обработки поверхности, форма и количество выступов, загрязнение, коррозия и др. факторы.
Обширные исследования потерь напора в турбулентном режиме выпол-нены в 1933 г. Никурадзе на гладких латунных трубах и трубах с регулярной искусственной шероховатостью из кварцевого песка. Им обнаружено существование трех областей движения, отличающихся характером влияния на коэффициент сопротивления числа Рейнольдса и шероховатости:
I – течение в гидравлически гладких трубах, при котором l зависит только от числа Рейнольдса;
II – течение в переходной области, где на l влияют и число Рейнольдса, и шероховатость;
III – течение в так называемых вполне шероховатых трубах, при котором l зависит только от шероховатости.
В области I, которой соответствуют малые числа Рейнольдса, движение жидкости в тонком пристенном слое является ламинарным и свойства поверхности не оказывают влияния на сопротивление. С увеличением ско-рости движения, т.е. числа Рейнольдса, начинает турбулизироваться пристен-ный слой жидкости, образуются вихри при обтекании выступов шерохо-ватости, которые являются причиной дополнительных потерь (область II). Наконец, при очень больших числах Рейнольдса основной вклад в сопро-тивление вносит вихреобразование в пристенном слое (область III).
В опытах других авторов на технических трубах с нерегулярной шеро-ховатостью в основном подтверждены результаты, полученные Никурадзе. Отличия состояли лишь в характере зависимости l=f(Re) в области II.
 |
На основе экспериментальных данных построены зависимости, представленные на рис.34.
Рис.34
Прямая 1 соответствует ламинарному движению жидкости. Коэффициент сопротивления по длине в этом режиме определяется по формуле Пуазейля
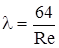 .
.
Прямая 2 соотетствует турбулентному движению жидкости в гидравлически гладких трубах. В этом случае используется формула Блазиуса
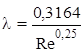 .
.
Коэффициент сопротивления вполне шероховатых труб определяется по формуле Шифринсона
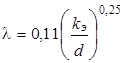 .
.
В переходной области используется формула Альтшуля
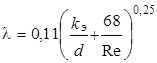 .
.
 |  |
Средние значения абсолютной эквивалентной шероховатости для некоторых новых технических труб приведены ниже:
цельнотянутые из цветных металлов 0,001
стальные бесшовные 0,014
стальные сварные 0,06
железные оцинкованные 0,15
чугунные без покрытия 0,3
Коэффициент Кориолиса для турбулентного режима движения жидкости находится в пределах α=1,05-1,1.
Дата добавления: 2015-11-26; просмотров: 1326;
