Уравнение неразрывности. Рассмотрим размещенный в потоке жидкости элементарный паралле-лепипед (рис.27)

Рассмотрим размещенный в потоке жидкости элементарный паралле-лепипед (рис.27).

z

x

Пусть проекции скорости движения жидкости в точке А на координатные оси составляют ux, uy, uz, а ее плотность r. На гранях параллелепипеда эти параметры равны:

– левая грань

.

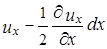
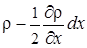– правая грань

.

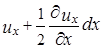
Разность массовых расходов жидкости через эти грани равна

Аналогичный вид имеют соотношения для остальных граней. Очевидно, что алгебраическая сумма масс жидкости, пронизывающих все грани параллелепипеда за время dt, равна убыли массы жидкости в его объеме

.

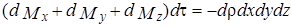После подстановок и сокращения получаем уравнение неразрывности для неустановившегосядвижения сжимаемой жидкости в окрестности точки А

.

Для установившегося движения сжимаемой жидкости

.

Для движения несжимаемой жидкости (r = Сonst)

.

Для элементарной струйки сжимаемой жидкости

а несжимаемой

.

При движении несжимаемой жидкости в каналах без источников и стоков

.

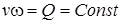Диффференциальные уравнения движения идеальной жидкости
(уравнения Эйлера в гидродинамике)

Уравнения движения могут быть получены из уравнений Эйлера для покоящейся жидкости (1-3), если, пользуясь принципом Даламбера, ввести в них плотность распределения силы инерции, численно равную ускорению

,

,

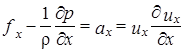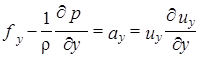так как

.

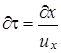Поскольку при интегрировании уравнений Эйлера появляются константы, для нахождения последних необходимо знать начальные и граничные условия, которые характеризуют распределение искомых параметров в начальный момент времени и их значения на границах потока в любой момент времени.

Умножив уравнения Эйлера соответственно на dx, dy, dz и учитывая, что

после сложения получим

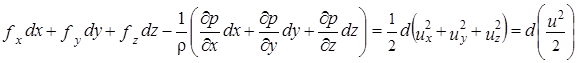. (12)