Волновое уравнение. Общее решение. Задача Коши и ее решение. Смешанная задача и ее решение

Перейдем в к безразмерным переменным:

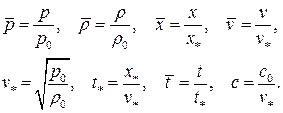
Выпишем для одномерного случая систему уравнений акустики, опустив штрих и черту над безразмерными переменными:

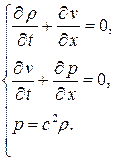
После перекрестного дифференцирования, использованного ранее при решении уравнений несжимаемой жидкости, можно получить волновое уравнениедля каждого из параметров , , :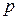

.

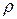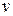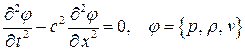Его общее решение имеет вид

.

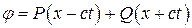В этом можно убедиться, если сделать замену переменных:

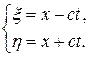
Тогда получим

.

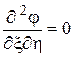Очевидно, решение последнего имеет вид

.

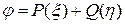Задача Коши для волнового уравнения. Поставим задачу Коши для волнового уравнения. Так как это уравнение второго порядка по времени, то необходимо для выделения искомого частного решения задать начальные условия для 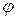и ее производной по времени 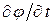. Таким образом, задача Коши имеет вид

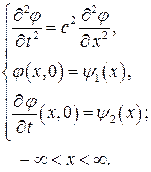
Решение задачи Коши дает формула Даламбера

.

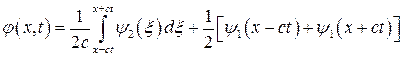Смешанная задача. Если решение волнового уравнения ищется на отрезке 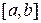, то необходимо задание граничных условий. Математическая постановка задачи формулируется следующим образом:

;

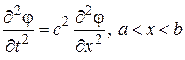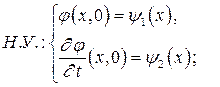
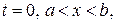
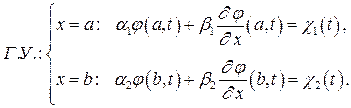
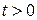
В частности, граничные условия могут быть заданы на полупрямой: 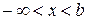, или .

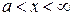Смешанная задача решается методами Фурье, преобразования Лапласа и другими. Когда аналитическое решение получить не удается, используют метод конечных разностей.