Условия на поверхности сильного разрыва. Ударная адиабата
3.4.1. Соотношения на разрыве в системе координат,
связанной с разрывом
По определению, функция 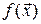 непрерывна в точке
непрерывна в точке 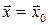 , если выполняется одно из трех равносильных между собой условий:
, если выполняется одно из трех равносильных между собой условий:
1) 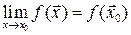 ;
;
2) 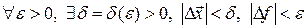 ;
;
3) 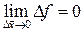 .
.
В противном случае говорят, что функция терпит разрыв в точке 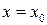 , а сама точка называется точкой разрыва. Для функции двух переменных точки разрыва могут образовывать линию, для функции трех переменных – поверхность.
, а сама точка называется точкой разрыва. Для функции двух переменных точки разрыва могут образовывать линию, для функции трех переменных – поверхность.
В механике сплошной среды выделяют поверхности слабого и сильного разрыва. Разрыв называется сильным, если на нем терпит разрыв какой-нибудь параметр сплошной среды. Разрыв называется слабым, если все параметры непрерывны, но производная какого-либо параметра терпит разрыв.
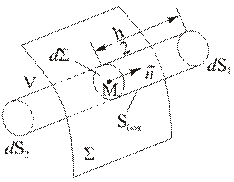 Рис. 3.4.1
Рис. 3.4.1
| Рассмотрим поверхность сильного разрыва 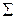 (Рис. 3.4.1). Предположим, что все параметры сплошной среды и их производные ограничены в рассматриваемой области течения. (Рис. 3.4.1). Предположим, что все параметры сплошной среды и их производные ограничены в рассматриваемой области течения.
|
Возьмем произвольную точку  на поверхности
на поверхности 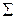 и получим условия на скачке (разрыве) в этой точке. При этом будем предполагать, что распределенные по поверхности
и получим условия на скачке (разрыве) в этой точке. При этом будем предполагать, что распределенные по поверхности 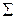 источники массы, импульса, энергии отсутствуют.
источники массы, импульса, энергии отсутствуют.
Направим нормаль 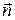 поверхности
поверхности 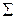 в точке
в точке  в направлении ее скорости
в направлении ее скорости 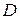 . Возьмем на поверхности
. Возьмем на поверхности 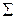 произвольную окрестность
произвольную окрестность 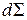 точки
точки  , в силу малости ее можно считать плоской. Отложим в обе стороны от
, в силу малости ее можно считать плоской. Отложим в обе стороны от 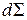 отрезки длиной
отрезки длиной 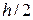 из каждой точки, принадлежащей
из каждой точки, принадлежащей 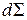 . Получим прямой цилиндр
. Получим прямой цилиндр 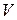 высоты
высоты 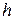 , ограниченный поверхностью
, ограниченный поверхностью 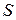 , состоящей из оснований
, состоящей из оснований 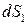 ,
, 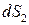 и боковой поверхности
и боковой поверхности 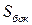
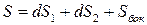 ,
,
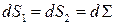 .
.
Цилиндр 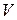 делится площадкой
делится площадкой 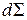 на два равных цилиндра
на два равных цилиндра 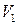 и
и 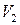 , ограниченных поверхностями
, ограниченных поверхностями 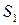 ,
, 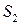 . Введем подвижную систему координат с началом в точке
. Введем подвижную систему координат с началом в точке  и движущуюся со скоростью
и движущуюся со скоростью 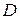 . Тогда цилиндр
. Тогда цилиндр 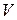 будет неподвижен в этой системе координат. Получим три вспомогательные формулы.
будет неподвижен в этой системе координат. Получим три вспомогательные формулы.
1. Докажем, что
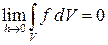 .
.
Справедливо равенство
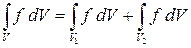 .
.
По теореме о среднем
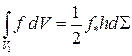 ,
, 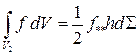 .
.
Подставляя значения интегралов и переходя к пределу при 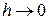 , получим искомую формулу.
, получим искомую формулу.
2. Можно доказать, что
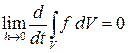 .
.
Действительно,
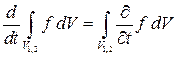
в силу неподвижности объемов 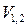 . Осталось применить формулу и учесть, что
. Осталось применить формулу и учесть, что
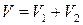 .
.
3. Обозначим 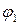 – значения параметра
– значения параметра 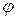 на
на 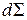 со стороны нормали
со стороны нормали 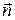 ,
, 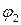 – значения на противоположной стороне
– значения на противоположной стороне 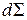 .
.
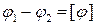 .
.
Докажем, что
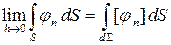 ,
,
где 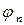 – проекция параметра
– проекция параметра 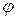 на внешнюю нормаль поверхности
на внешнюю нормаль поверхности 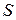 .
.
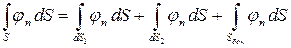 ,
,
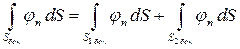 .
.
По теореме о среднем
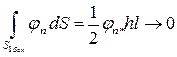 , при
, при 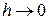 ,
,
где 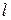 – длина границы площадки
– длина границы площадки 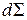 . Аналогично можно убедиться, что второй интеграл также стремится к нулю. Поэтому
. Аналогично можно убедиться, что второй интеграл также стремится к нулю. Поэтому
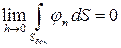 .
.
Далее,
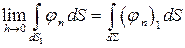 ,
,
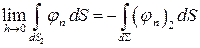 ,
,
поскольку нормали 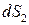 и
и 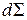 направлены в противоположные стороны, а
направлены в противоположные стороны, а
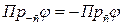 .
.
Суммируя, получим искомую формулу.
Дата добавления: 2015-12-29; просмотров: 1522;
