Решение уравнений акустики

Так как волновое уравнение является эквивалентом системы уравнений акустики, то его решение может быть использовано для нахождения решений уравнений акустики. Применим общее решение к плотности жидкости. Тогда

.

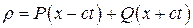Согласно акустическому уравнению состояния 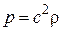имеем

.

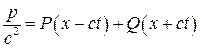Найдем скорость среды 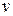из уравнения неразрывности:

,

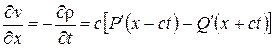где штрихом обозначено дифференцирование по 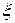и 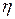соответственно. Интегрируя по 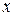, получим

.

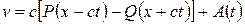Для определения произвольной функции 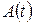, зависящей от времени, используем уравнение импульсов. Получим

.

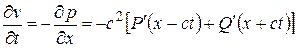С другой стороны

.

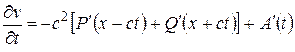Приравнивая правые части уравнений, видим, что

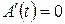, т.е. .

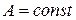Итак,

, .

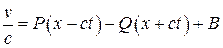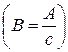Значение постоянной 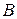определяется после постановки конкретной задачи из начальных и граничных условий, как правило .

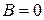Запишем решение уравнений акустики в исходных размерных переменных и при :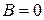

,

,

.

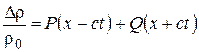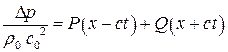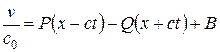Для волны, бегущей вправо 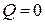. Следовательно,

.

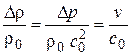Условия малости возмущения, соответственно, принимают вид

, , .

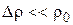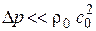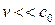Так, например, для воды 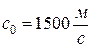, 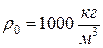и .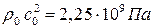

Следовательно, при 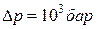возмущение в воде еще можно рассматривать как малое и пользоваться линейной теорией. Заметим, сначала мы предположили, что возмущение давления мало по сравнению с начальным давлением. Теперь ясно, что это требование является слишком сильным. Достаточно предположения, что возмущение плотности мало по сравнению с начальным ее значением.