Nbsp;   Решение. Упростим схему, используя метод эквивалентных преобразований.

Упростим схему, используя метод эквивалентных преобразований.

Сначала несимметричную звезду без нулевого провода заменим эквивалентным треугольником сопротивлений:

Z_ab1 = jwL + r + 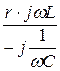= j10 + 10 + 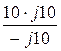= j10 Ом,

Z_bc1 = r – j 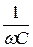+ 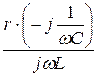= 10 – j10 + 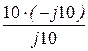= -j10 Ом,

Z_ca1 = jwL – j 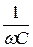+ 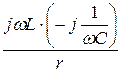= j10 – j10 + 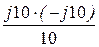= j10 Ом.

Теперь два треугольника сопротивлений оказываются включенными параллельно (рис. 4.24,а).

Эти два треугольника можно заменить одним с сопротивлениями фаз

Z_ab = 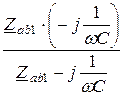= = 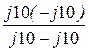¥, следовательно, в этом параллельном контуре без потерь наблюдается резонанс токов и входное сопротивление этого контура бесконечно большое (разрыв цепи по отношению к остальной схеме);

Z_bс = 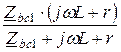= = 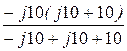10 – j10 Ом;

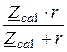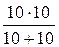Z_са = = = 5 Ом.

В результате получаем схему замещения нагрузки, подключенной на зажимы a-b-с, представленную на рис. 4.24,б.

Представим, что обмотки симметричного трёхфазного источника ЭДС соединены в звезду с ЭДС Е = 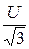= = 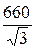380 В = Е_А.

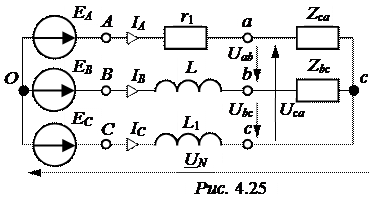
Получаем преобразованную схему рис. 4.25. Для этой схемы

U_N = = =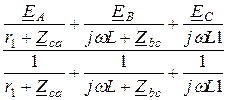

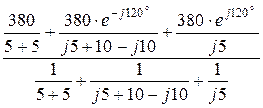= 200 + j225 B.

Линейные токи генератора

I_А = 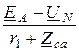= = 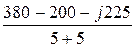18 – j22,5 A;

I_B = 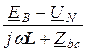= = 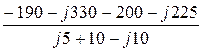-39 – j55,5 A;

I_C = 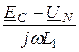= = 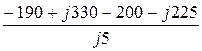21 + j78 A.

Линейные напряжения на зажимах приёмников на основании схемы рис. 4.25:

U_ab = I_А×Z_ca – I_B×Z_bc = (18 – j22,5)×5 – (-39 – j55,5)×(10 – j10) = 1035 + j52,5 B;

U_bc = I_B×Z_bc = (-39 – j55,5)×(10 – j10) = -945 – j165 B;

U_ca = -I_A×Z_ca = -(18 – j22,5)×5 = -90 + j112,5 B.

Возвращаемся к исходной схеме рис. 4.23 и находим фазные токи треугольника I_ab = 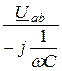= = 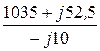-5,25 + j103,5 A;

I_bc = 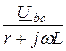= = 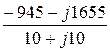-55,5 + j39 A;

I_ca = 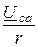= = 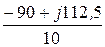-9 + j11,25 A.

Линейные токи треугольника I_a = I_ab – I_ca = 3,75 + j92,25 A;

I_b = I_bc – I_ab = -50,25 – j64,5 A;

I_c = I_ca – I_bc = 46,5 – j27,75 A.

Токи приёмника, соединённого в звезду, рассчитаем по I закону Кирхгофа: I_a1 = I_A – I_a = 14,25 – j114,75 A;

I_b1 = I_B – I_b = 11,25 + j9 A;

I_c1 = I_C – I_c = -56,5 + j105,75 A.

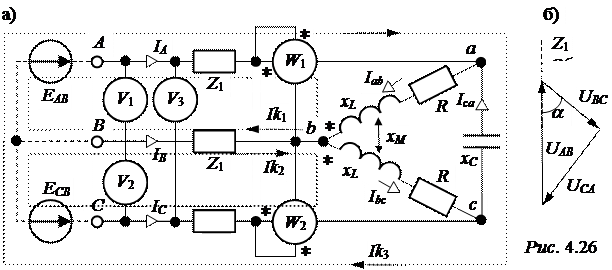
ЗАДАЧА 4.20. В схеме рис. 4.26,а определить токи во всех ветвях, если показания вольтметров: U₁ = 220 В, U₂ =127 В, U₃ =191,3 В, а Z₁ = 3 + j4 Ом, R = 20 Ом, x_L = 30 Ом, x_M = 25 Ом, x_C = 40 Ом. Рассчитать показания ваттметров и сравнить их с тепловыми потерями в треугольнике нагрузки.

Дано: U1 := 220 U2 := 127 U3 := 191,3 ORIGIN := 1 j :=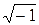

Z1 := 3 + j4 R := 20 xL := 30 xM := 25 xC := 40

Используя теорему косинусов, с помощью качественно построенной векторной диаграммы линейных напряжений (рис 4.26,б) определим их комплексы, совместив с вещественной осью UAB:

a := acos 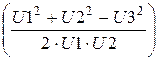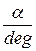= 60.008

UAB := U1 UBC := U2×e ^{j×(a -p)} UCA := – UAB – UBC

Проверка: |UCA| = 191.3

Припишем систему линейных напряжений двум ЭДС (рис. 4.26,а) EAB = UAB и ECB = -UBC, а расчёт токов в этой схеме произведём методом контурных токов. Определим собственные и взаимные комплексные сопротивления контуров

Z11 := 2×Z1 + R + j×xL Z22 := 2×Z1 + R + j×xL Z33 := 2×Z1 – j×xC

Z12 := – Z1 – j×xM Z13 := Z1 Z23 := Z13

Матрицы контурных сопротивлений, ЭДС и токов

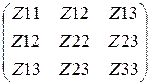Zk := Ek := 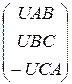Ik := Zk ^-1×Ek Ik =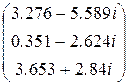

Токи в ветвях IA := Ik₁ + Ik₃ IB := Ik₂ – Ik₁ IC := – Ik₂ – Ik₃

Iab := Ik₁ Ibc := Ik₂ Icz := – Ik₃

Показания ваттметров

Uab := UAB + Z1×(IB – IA) Ucb := – UBC + Z1×(IB – IC)

P1 := Re(Uab× 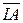) P2 := Re(Ucb× )

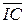Тепловые потери в треугольнике Pt := R×(|Iab|² + |Ibc|²)

Ответы IA = 6.929 – 2.749i Iab = 3.276 – 5.589i

IB = -2.925 + 2.965i Ibc = 0.351 – 2.624i

IC = -4.004 – 0.216i Ica = -3.653 – 2.84i

P1 = 1.222´10³ P2 = -242.909 P1 + P2 = 979.437 Pt = 979.437

Сумма показаний ваттметров равна тепловым потерям в треугольнике нагрузки. Таким образом, ваттметры, включенные по представленной схеме, измеряют активную мощность нагрузки.