Nbsp;   Каноническая форма записи задачи линейного программирования

Каноническая задача линейного программирования отличается от задачи программирования общего вида тем, что ограничения в ней заданы в виде системы уравнений:

_.

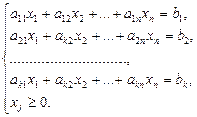
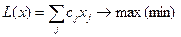Для решения такой системы выделяют базисные и свободные переменные и получают общее решение, в котором свободные переменные выступают как произвольные постоянные, а базисные – как функции обмена.

Определение. Решение основной задачи линейного программирования называется базисным или опорным, если все свободные переменные равны нулю, а базисные не отрицательны.

Если система ограничений представляет собой совокупность уравнений и неравенств или только неравенств, задача не является канонической.

В этом случае все неравенства приводят к уравнениям, вводя новые (балансовые) переменные в каждое неравенство системы.

Балансовые переменные положительны, их экономический смысл в том, что в решении они показывают либо остатки ресурсов, либо избытки при данном оптимальном решении.

Пример. Задана система ограничений, привести ее к каноническому виду

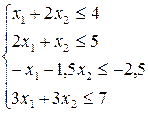
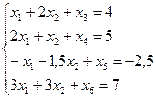
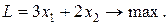
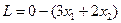
Добавим в каждое из них по одной новой (балансовой) переменной. Получим каноническую задачу линейного программирования.

Существует несколько методов решения задач ЛП, два основных из них симплексный и графический методы.