АЛГОРИТМ ПРЕОБРАЗОВАНИЯ ЭЛЕМЕНТОВ СИМПЛЕКСНОЙ ТАБЛИЦЫ

Пусть целевая функция (3.5) и система ограничений (3.6) разрешены относительно базисных переменных через свободные.

Введём дополнительные обозначения:

x_i – базисные переменные ; y_i – свободные переменные; вместо a_ij = S_ij; вместо b_i = S_i0; c_j = S_{m+1, j}

Алгоритм пересчёта элементов симплексной таблицы при замене базисной переменной x_r на свободную y_k.

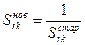- для разрешающего элемента (3.12)

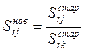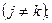, - для разрешающий строки (3.13)

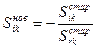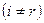, - для разрешающего столбца (3.14)

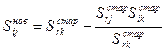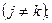
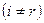, - для всех оставшихся элементов (3.15).

Строка r, соответствующая переменной, выводимой из базиса, называется разрешающей строкой.

Столбец k, соответствующий переменной вводимой в базис называется разрешающим.

Элемент r_k называется разрешающим элементом.

Алгоритм поиска симплекс метода состоит из 2-х этапов:

1. поиск опорного решения (А ® С)

2. поиск оптимального решения (В ® С)

А – алгоритм выбора разрешающего элемента при поиске опорного.

В – алгоритм выбора разрешающего элемента при поиске оптимального решения.

С – коэффициент пересчёта коэффициентов симплексной таблицы по соотношению (9).

АЛГОРИТМ ВЫБОРА РАЗРЕШАЮЩЕГО ЭЛЕМЕНТА ПРИ ПОИСКЕ ОПОРНОГО РЕШЕНИЯ

Проводим анализ столбца свободных членов. Если все свободные члены являются положительными, то решение является опорным. Пусть какой-то элемент из столбца свободных членов имеет отрицательное значение, тогда проводим анализ элементов этой строки: если среди остальных элементов строки нет отрицательных значений, то система несовместна и не имеет решения. За разрешающий выбирается столбец с наибольшим по модулю отрицательным значением в соответствующей строке, который будем обозначать “k”.

Разрешающая строка определяется по дополнительному соотношению:

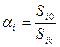(3.16),

где S_i0 – свободный член i-ой строки;

S_ik – коэффициент разрешающего столбца;

В качестве разрешающей выбирается та строка, которая имеет минимальное положительное a. Разрешающую строку будем обозначать как “r”.