ОБЩАЯ ЗАДАЧА МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Одним из методов математического моделирования является математическое программирование.
Математическое программирование – это раздел математики, в котором изучаются и разрабатываются теоретические положения и конкретные численные методы для решения задач принятия оптимальных решений (или на языке математики – экстремальных задач с ограничениями). Т.о. Математическое программирование – это процедура последовательного приближения к наилучшему решению.
Т.е. математическое программирование занимается исследованием свойств и разработкой методов решения задач следующего вида: найти значения переменных 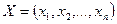 , принадлежащему некоторому заданному множеству G и доставляющих максимум или минимум заданной функции
, принадлежащему некоторому заданному множеству G и доставляющих максимум или минимум заданной функции 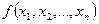 этих переменных.
этих переменных.
А также имеется дополнительное ограничение
xj ³ 0 , 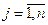 (3.2)
(3.2)
Если целевая функция на допустимом множестве G имеет единственный экстремум (единственное оптимальное решение), то задача называется одноэкстремальной.
В многоэкстремальных задачах целевая функция имеет несколько локальных экстремумов. Наиболее значительный из них - глобальный экстремум.
(Мы будем рассматривать одноэкстремальные задачи).
В зависимости от вида целевой функции и математических выражений, входящих в систему ограничений, математическое программирование разделяют на 2 основных типа.
1. если целевая функция и все выражения системы ограничений являются линейными (содержат неизвестные только первой степени), то математическое программирование называется линейным программированием.
2. если в математической модели целевая функция или хотя бы одно из ограничений системы нелинейны, программирование называется нелинейным.
Наиболее разработанной и простой частью математического программирования является линейное программирование в силу достаточной изученности линейных функций и возможности прогнозирования их поведения.
Задачи линейного программирования (ЛП) всегда одноэкстремальны, причем экстремум достигается на границе допустимой области.
Любая задача максимизации max[f(x),G(x)] может быть представлена задачей минимизации, характеризующейся min[-f(x),G(x)] при этом оптимальное решение будет одно и тоже.
Математическая формулировка задачи ЛП.
Пустьимеется целевая функция 
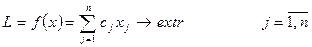
и имеется система ограничений G и дополнительное ограничение.
Тогда существует два вида математической формулировки задачи линейного программирования.
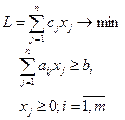 |
1. Задача минимизации расходов
2. Задача максимизации прибыли
Дата добавления: 2015-12-22; просмотров: 3099;
