Аддитивность информации в задачах распознавания

Постановка задачи:

1. Пусть заданы алфавит классов Q_i, i=1,…,m;

2. Априорные вероятности появления объектов различных классов P(Q_i),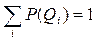

3. Словарь признаков {X_j}, j=1,…,n;

4. Частные распределения f_i(x_j);

5. Совместные Ф⁽ⁱ⁾j1,…,Ф⁽ⁱ⁾jr, (x_j₁,…,x_jr), j1,…,jrÎ1,…,n;

6. Условные плотности распределений некоторых совокупностей признаков: f⁽ⁱ⁾_j₁,…,jr(x_j/x_j₁,…,x_jr).

Требуется установить:

1) является ли статистическая независимость признаков

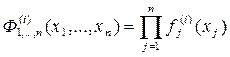
достаточным условием равенства безусловной I(X_j) и условной I(X_j/x_j₁,…,x_jr) информативности признаков или, что равносильно, достаточным условием аддитивности информации, т.е.:

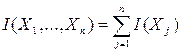
Если то не так, то какие дополнительные условия необходимы для того, чтобы это свойство имело место;

2) является ли статистическая независимость признаков

необходимым условием аддитивности информации, иначе, возможно ли выполнение равенства I(X₁,…,X_n) для некоторой совокупности статистически зависимых признаков.

Доказательство:

1. Исходная энтропия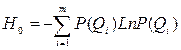

2. После измерения признака X_j энтропия H(X_j) в системе распознавания

равна: ,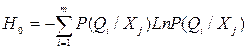

где 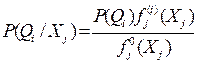- апостериорные вероятности отнесения распознаваемого объекта к классу Q_i.

Среднее значение энтропии H(X_j) определяется интегрированием H(X_j) по всей области w_j возможных значений X_j с весом f⁰_j(X_j), т.е.

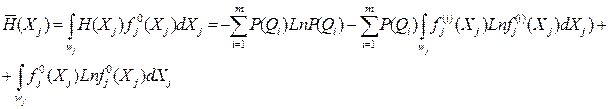
Одну из интерпретаций информативности признака X_j как

I^|(X_j)=H₀-H(X_j)

можно вычислить как разность энтропии распределения 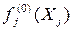и средней энтропии распределений :

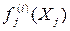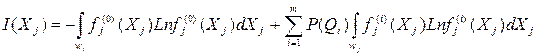
Аналогично совместная информативность признаков X_j и X_k равна:

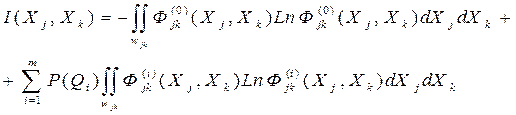
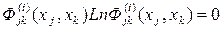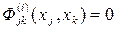Если принять, что при , то под областью w_jk можно понимать всю плоскость (x_j,x_k). Тогда имеем:

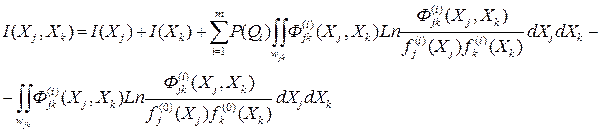
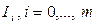
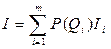
Если все I_i = 0, включая и I₀, то действительно

I(X_j,X_k)=I(X_j) + I(X_k)

Таким образом, само по себе условие статистической независимости признаков x_j и x_k, не является достаточным для аддитивности информации.

Вместе с тем необходим отбор и формирование достаточной совокупности информативных признаков.

Потенциально возможное количество информации, получаемое от измерительных устройств, равно (применительно к одному признаку):

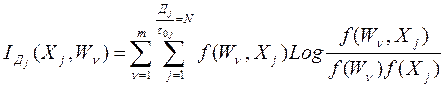
где Д_i – диапазон изменения j-го признака;

t₀_j – образцовая измерительная величина;

X_j – дискретное значение j-го признака, j=1,…,Д_j/t₀_j;

W_n - n - тый источник информативности W-го объекта.

В качестве критерия значимости вводится некоторая величина I⁽^j⁾_H – информативность признака X_j, причем:

1) при I⁽^j⁾_H>I⁽^g⁾_H, (j¹g) вероятность правильной идентификации выше с

использованием X_j ,чем с X_g;

2) достоверность идентификации при использовании должна быть

линейной (монотонной) функцией суммы I⁽^j⁾_H для признаков в X.

Необходимо, чтобы I⁽^j⁾_Hбыла выбрана как среднее некоторой функции, находящейся в соответствии с информационным критерием идентификации и статистическими характеристиками контролируемого реального канала наблюдения объектов w_n, n=1,…,r.

Этим условиям удовлетворяет величина:

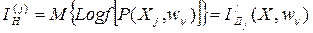являющаяся взаимной информацией признака X_j и контролируемых объектов w_n.

С условием нормировки эта величина I⁽^j⁾_H может быть представлена как:

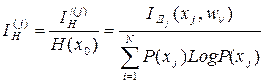
где Н(х) – исходная энтропия для внешней среды;

P(x_j) – закон распределения вероятности для x_j.

С другой стороны, значимость (добротность) признака для поэкземплярной идентификации w_n выражается относительным расхождением между гипотезами при априорном знании распределений P(x/w_n), P(x) и P(w_n).

Для статистически независимых признаков критерий расстояния S_jk удовлетворяет всем требованиям для I⁽^j⁾_H, кроме условия нормировки, и для r экземпляров источников информации (w_n) он может быть представлен как:

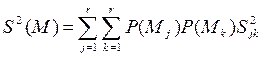где M_j, M_k – векторы среднего для x_j, x_k.

Величина S²_jk для нормального закона относительно P(x/w), P(x) и P(w) соответственно равна:

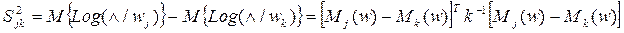
где 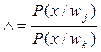, где j¹k – отношение правдоподобия.

k^-1 – обратная коррелированная матрица.

<4 5 678 9 10 >

Дата добавления: 2016-01-20; просмотров: 1716;