Формальное представление описаний

Рассмотрим формальные системы, в рамках которых описания изображений (сцен) могут порождаться и записываться.

Синтаксические описания.

Пример простой сцены, изображающей коробку и цилиндр.

а) грубое описание – “коробка и цилиндр”;

б) введем структуру сцены, тогда и “коробка слева от цилиндра”;

в) уточняем описание, охарактеризуем коробку как соединение 3-х четырехугольников, т.е. до любого желаемого уровня детальности.

Этот процесс последовательного уточнения структурного описания сцены носит заметное сходство с процессом получения структурного описания английского предложения.

В соответствии с этим естественно рассмотреть понятие грамматики.

Определение:

1. Грамматика – некоторая формальная система, в рамках которой можно

описывать изображение. При этом используется синтаксический подход (лингвистический, структурный) как совокупность теоретических методов, потенциально применимых к задачам анализа сцен.

2. С этих позиций – грамматика – формальная конструкция, содержащая

образования 3-х типов:

- терминальные (первичные) символы;

- нетерминальные (вторичные) символы;

- правила подстановок (порождающие правила).

Грамматика может использоваться либо в порождающем, либо в

анализирующем режиме (т.е. синтез и анализ).

Порождающий режим: позволяет конструировать строки терминальных символов путем последовательного применения правил подстановок.

Определение: Строка терминальных символов, построенная с помощью данной грамматики, называется предложением. Множество предложений, которые могут быть построены с помощью данной грамматики, называются языком данной грамматики.

Следствие: Таким образом, образы для сцен строятся из соединенных различными способами подобразов так же, как фразы и предложения строятся путем соединения слов, а слова составляются из букв.

Анализирующий режим:

Пример 1: Пусть дано множество терминальных символов T={a,b} и множество нетерминальных символов N={S,B}, где символ S означает “предложение” (sentence) и, таким образом, отличается от других нетерминальных символов.

Эта иллюстративная грамматика содержит пять правил подстановки:

1) S::=a;

2) S::=aS;

3) S::=aB;

4) B::=b;

5) B::=bS.

1) Когда грамматика используется в порождающем режиме, символ

“::=” имеет смысл “заменить символ слева строкой символов справа”.

Применим грамматику для построения простого предложения. Начнем с того, что приравняем символ, означающий предложение, самому себе:

S = S,

Выберем правило (2), применим его к правой части равенства: S = aS.

Применим правило (2) еще раз: S = aaS.

Применим правило (3): S = aaaB.

Применим правило (5), получим: S = aaabS.

Применим правило (1): S = aaaba.

В примере дальнейшие подстановки невозможны. Таким образом, применение порождающих правил к исходному символу предложения S, порождается последовательностью терминальных символов. Применение правил в другой последовательности даст другую последовательность символов.

2) Рассмотрим случай, кода грамматика используется в

анализирующем режиме. Пусть анализируются строки первичных символов. Тогда нужно ответить на 2 вопроса:

а) – является ли данная строка предложением языка, определяемого грамматикой?;

б) – какова структура строки, если она является предложением?

Определение: Анализ ответов посредством использования грамматики, т.е. реализация анализирующего режима называется грамматическим разбором. Один из методов разбора, называемый разбором сверху вниз, основан на конструировании дерева всех возможных способов, посредством которых можно применять правила подстановки для построения стоящей на первом месте исходной строки.

Следствие 1: Распознавание здесь состоит в синтаксическом анализе, или, иначе, грамматическом разборе “предложения”, описывающего данный объект.

Следствие 2: Если нельзя найти такую последовательность правил, строка не является предложением, а если имеется единственная последовательность, то полный путь по дереву определяет структуру строки. Если имеется более чем одна последовательность правил, то структура строки синтаксически неоднозначна.

Пример 2: Пусть анализируется предыдущая строка из примера, т.е. aaaba, которая конечно же является предложением. Поскольку она начинается с “a”, то к ней применимы только первые три правила. Потому строка имеет форму либо “a” либо “aS”, либо “aB”. Можно было бы ту строку отнести и к форме “aB”, если бы мы не видели, что все формы “B” начинаются с символа “b”. Потому наша строка не может иметь форму “aB”. Следовательно, строка должна иметь форму “aS”, где теперь S = aaba.

Пример 3: Представим наш анализ из примера 1 в виде дерева грамматического разбора:

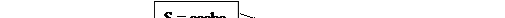
1 3

1 3

Цифры на ветвях – это номера правил. Узлы помечены крестом, если для них нет применимых правил подстановок.

В примере 3 законченное дерево определяет последовательность правил подстановок 2,2,3,5,1, которая использовалась для порождения исходной строки. В этом примере имеется только один путь через дерево, следовательно, предложение aaaba порождается грамматикой единственным образом. Здесь язык грамматики состоит из всех последовательностей символов “a” и “b”, начинающихся с “a” и не содержащих нигде двух символов “b” подряд.

Более общие случаи имеют гораздо большую сложность анализа. Это уже относится к теории формальных языков.

Определение: Основная теоретическая трудность, связанная с применением синтаксических методов к двумерным сценам, проистекает из следующего фундаментального факта: одномерная линия упорядочена естественным образом, а двумерная плоскость – нет! Следовательно, естественный способ обработки одномерной строки символов заключается в замене одного символа другим по цепочке. Никакой естественной аналогии двумерного случая не существует. Построим дерево для нашего предыдущего рисунка для разбора этой сцены (коробка и цилиндр).

подобраз

подобраз подобраз

Синтаксический подход к распознаванию образов дает возможность описывать большее множество сложных объектов путем использования небольшого множества непроизводных элементов и грамматических правил.

Однако, даже если мы указали точные описания для таких первичных элементов как “поверхность”, это дерево будет описывать сцену весьма смутно (неоднозначно). Например, три поверхности можно соединить вместе различными способами, и только некоторые из них образуют коробки.

Проблему отсутствия естественного упорядочения для плоскости пытались решить различными путями.

Наиболее простой путь состоит в том, чтобы опираться только на границу объекта, пользуясь естественным упорядочением одномерного множества точек. Пример 4: определения четырехугольника (коробки): четырехугольник:: = линия + линия + линия + линия, где знак “+” означает сцепление и подразумевается, что цепочка должна замкнуться на себя. Здесь выбор первичных элементов в виде прямых линий очевиден.

Для объектов с кривыми поверхностями неизвестно, где кончается один элемент и начинается другой. Такого рода трудность свойственна всем синтаксическим методам.

В нашем простом примере еще нужно записать отношения между четырехугольниками. Можно задать “крюки” или точки притяжения на каждом четырехугольнике.

Другой метод задания отношения между первичными элементами также основан на стандартных точках притяжения, в частности, на предположении, что каждый первичный элемент имеет две характерных точки – голов и хвост.

Следствие: Сцеплению двух терминальных символов придается смысл сложения векторов, что распространяется и на более сложные конструкции.

Пример 5: Имеются терминальные символы a,b,c. Тогда нетерминальная точка А как A = a+b+c будет иметь в качестве хвоста хвост элемента а, а в качестве головы – голову элемента с. Т.е. формальная система, имеющая дело со сцеплением (или с анализом) терминальных символов, пригодна также и для нетерминальных.

Операция сцепления головы с хвостом обозначается “+”, а операция поменять хвост на голову – знаком “~”.

Одним из наиболее перспективных аспектов той возможности является использование рекурсивной природы грамматики.

a b c d a a a

d b

c c c

Грамматическое правило (правило подстановки) может быть применено любое число раз, так что оказывается возможным очень компактно выразить основные структурные характеристики бесконечного множества предложений.

Практическая полезность подхода определяется способностью распознавать терминальные элементы образов и их взаимные отношения, выраженные операциями композиции.

Определение: Конкатенацией элементов, например, a и b, называется составленная из них цепочка.

Пример 6: Если в качестве единственного отношения (т.е. операции композиции) для описания образов выбрать конкатенацию, то при терминальных элементах прямоугольник (поверхность) будет представлен цепочкой aaab, cccd. Здесь “+” обозначает операцию конкатенации при сцеплении одного элемента с другим по принципу “ голова с хвостом”.

Пример 7: Кроме цепочной может быть представлена древовидная структура композиции, например, цифры 9:

a a

d b

c c b

b

c c подобраз

подобраз

c + c + d + a + a + b b + b + c + c

Другим представлением структурной совокупности информации образа служит граф отношений:

Пример:

a c

f d

b l

F

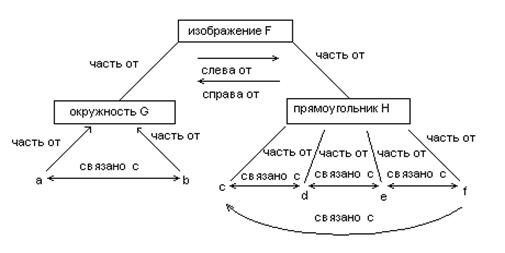
Следствие 1: Поскольку между графом и матрицами существует взаимно однозначное соответствие, граф отношений также может быть выражен через “матрицу отношений”.

Путем использования графа отношений для писания образа можно расширить класс допустимых отношений, включив в него любое отношение, которое удобно(просто) определяется из образа.

Следствие 2: Конкатенация – единственная естественная операция для одномерных языков.

Следствие 3: Граф, вообще говоря, содержит циклы, в то время как дерево их не содержит. Поэтому с помощью графа может быть составлено более сложное описание, хотя при помощи древовидных структур возможно непосредственное использование методов теории формальных языков и задачи компактного представления и анализа изображений, имеющих существенное структурное содержание.