Для оценки плотности в некоторой точке методом “парзеновского окна” подсчитывается количество объектов, попадающих в фиксированную малую окрестность .

Эта окрестность 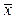выбирается таким образом, что с увеличением N ее объем V_N уменьшается. Если при N®¥ V_N®0, k®¥ и k/N®0, то оценка плотности в точке 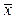является состоятельной.

Этим условиям удовлетворяют многие виды зависимостей, например:

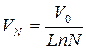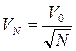; и т.д.

Тогда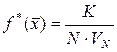

Средняя эмпирическая плотность 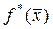в окрестности точки используется также и для оценки плотности методом “K_N ближайших соседей”. Только в отличие от метода “парзеновского окна” (где к – величина случайная) здесь “K_N ближайших соседей” определяются как функция от N, причем окрестность 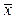берется таких размеров, чтобы включать ровно K_N ближайших объектов.

В зависимости от значений K_N к N предъявляются аналогичные требования:

- при N®¥ необходимо, чтобы K_N®¥ и K_N®0, именно это обеспечивает сходимость оценки в точке ;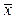

- при определении K_N можно использовать те же функции, т.е. K_N=LnN, 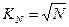и т.д.

Методы “парзеновского окна” и “обобщенной гистограммы” являются

по сути дела “локальными” аналогами гистограмм, построенных соответственно при равных интервалах разбиения и при условии попадания в них примерно одинакового числа реализаций.

Основное неудобство:

- неопределенность в выборе зависимостей V_N от N и K_N от N;

- методы непараметрического оценивания в целом хороши только при

достаточно больших выборках (при малых выборках об их качествах трудно что-либо утверждать).

На практике часто прибегают к эвристическому конструированию

(формированию) функций плотности 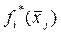, j=1,…,n, I=1,…,m и функций P(Q_i), основанному на экспертных оценках:

- определяется группа экспертов (веса для которых B_k, k=1,…,t),

оценивающих возможные значения признаков x_j объектов всех классов;

- каждый из экспертов А_к сообщает значение признака как C_K(X_j/Q_i), при

этом некоторые из значений признака x_j объектов класса Q_i, указанные разными экспертами, могут совпадать, т.е. C_g(X_j/Q_i) = C_q(X_j/Q_i), g,qÎ1,…,t; кроме того некоторые эксперты могут указать на несколько возможных значений признака X_j в i-том классе Q_i, т.е.:

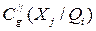, и т.д.;

необходимо учитывать также, что некоторые эксперты “промолчат” (указания 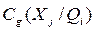отсутствуют);

- определяется усредненный вес мнений экспертов группы L₀(X_j/Q_i):

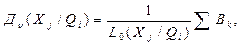
A_kÎL_n(X_j/Q_i)

где L_n(X_j/Q_i) – группа экспертов; n = 1,…,r(X_j/Q_i);

L₀(X_j/Q_i) – число экспертов в группе L_n;

Алгоритм: группа экспертов L_n(X_j/Q_i) указала, что значение признака X_j в классе Q_i составляет С_n(X_j/Q_i).

Следствие: Статистическая вероятность того, что значение признака X_j у объектов, принадлежащих классу Q_i равна величине С_n(X_j/Q_i) указанной группой экспертов L_n(X_j/Q_i), пропорциональна усредненному весу мнений этой группы, т.е.:

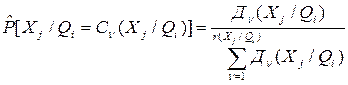
Это соотношение позволяет сформировать статистические ряды:

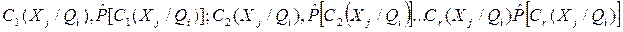
а на их основе путем сглаживания определить оценки искомых функций распределения вероятностей .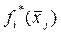

Метод определения функций P(Q_i) аналогичен.

Следствие: Таким образом, эвристический подход к формированию априорных сведений основывается на обработке результатов опроса группы экспертов с учетом их авторитета (веса).