Эмпирические методы распознавания
Характерной чертой параметрического случая является использование в той или иной степени эмпирических распределений вероятности вместо истинных и эмпирических оценок (средних) вместо математических ожиданий. Это обстоятельство приводит к особым требованиям к объему и составу полной совокупности исходных данных {X} для того, чтобы эмпирическое осреднение приводило к состоятельным оценкам математических ожиданий.
К непараметрическим методам оценки плотности вероятности f(xj) прибегают также при большом числе признаков xj и наличии зависимостей между ними. В этом случае нет необходимости делать предположение о виде функции f(xj). При этом класс функций, к которым применимы эти методы, ограничивается непрерывными функциями или близкими к ним.
Оценка парзеновского типа (обобщенная гистограмма)
Это одна из распространенных непараметрических оценок. Оценочная функция при этом может быть представлена выражением:
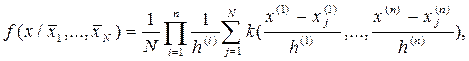
где  ,j=1,…,N – функции, называемые ядрами, центрами которых являются точки в пространстве признаков, соответствующие объектам обучающей выборки.
,j=1,…,N – функции, называемые ядрами, центрами которых являются точки в пространстве признаков, соответствующие объектам обучающей выборки.
h(i) – коэффициент “размытости” i-го признака, зависящий от N.
Если ядра выбираются симметричными относительно центра, т.е. являются функциями расстояния от центра, то оценка принимает вид:
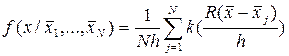
где 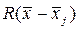 - расстояние от
- расстояние от 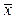 до
до 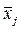 .
.
Обобщенная гистограмма является асимптотически несмещенной и состоятельной, если выбор функции h от N при N®¥ обеспечивает h®¥ и Nh®¥.
Для получения оценки плотности не по всему пространству признаков, а в заданной точке используются методы локального оценивания парзеновского окна и KN “ближайших соседей”.
Оба метода основываются на возможности оценивания вероятности появления реализации в заданной области по эмпирической частоте.
Вероятность попадания в некоторую область А признакового пространства “K” объектов из выборки объемом N равна:
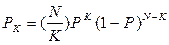
где Р – вероятность попадания в эту область одного объекта.
Математическое ожидание к (как случайного числа объектов, попадающих в область А) равно P×N. Распределение вероятности Pk имеет выраженный максимум около математического ожидания. Потому можно полагать, что k@PN.
То равенство тем точнее, чем больше N.
Определение: Чтобы получить оценку средней плотности по области А необходимо найти значение Р как:
P @ k/N
И поделить то значение оценки вероятности на объем VA области А, т.е.:
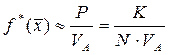
Дата добавления: 2016-01-20; просмотров: 863;
