Обучающие системы распознавания

В теории и практике построения систем распознавания значительная роль принадлежит задаче обучения, состоящей а наилучшем описании классов объектов на языке признаков в условиях дефицита исходной информации. При этом под “наилучшим” понимается такое описание классов, при котором обеспечивается наибольшая точность (достоверность) распознавания неизвестных объектов.

В настоящее время большое внимание уделяется проблеме создания обучающих систем, т.е. таких систем, которые способны с течением времени улучшать свое функционирование.

Таким образом, необходимость в применении обучающихся систем возникает в тех случаях, когда система должна работать а условиях неопределенности и имеющаяся априорная информация настолько мала, что отсутствует какая-либо возможность заранее спроектировать систему с фиксированными свойствами, которая работала бы достаточно хорошо.

Принцип построения обучающихся систем основан на использовании процессов обучения, осуществляемых вероятностными итеративными алгоритмами, именуемыми алгоритмами обучения, позволяющими в результате обработки текущей информации восполнить недостаток априорной информации и, в конечном итоге, достигнуть наилучших, с определенной точки зрения, показателей качества работы.

Цель обучения. В общей форме цель представляет собой то состояние, к которому должна прийти система в результате обучения.

Выделение этого состояния, по существу, сводится к выбору некоторого функционала, экстремум которого отвечал бы тому состоянию. Изменение состояния системы достигается изменением внешнего управляющего воздействия либо изменением параметров системы.

Введем вектор: С = (С₁,…,С_N), компоненты которого представляют собой значения характеристик управляющего воздействия либо значения параметров. Тогда в качестве функционала можно выбрать функционал вектора С вида:

,

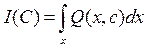где х = (х₁,…,х_М) – вектор случайного стационарного дискретного или непрерывного процесса, плотность распределения которого равна Р(Х), а Q(X,C) – для каждой реализации Х случайный функционал, математическое ожидание которого равно I(C).

То есть, иначе: I(C) = M{Q(X,C)}.

Условие экстремума в этом случае: ÑI(C) = M_X{Ñ_C×Q(X,C)} = 0.

Неполнота априорной информации, состоящая в том, что заранее неизвестно ни отношения правдоподобия, ни априорные вероятности, является серьезным препятствием для применения классических подходов, например, Байесова. Именно в этих случаях обучающиеся системы способны после некоторого периода обучения выработать решающее правило и произвести распознавание или классификацию. Незнание здесь преодолевается обучением. Чем меньше априорная информация, тем больше времени необходимо для обучения. Это – плата за незнание.

Различают два вида обучения:

- с поощрением;

- без поощрения (самообучение).

Обучение с поощрением (с учителем)

Для построения решающего правила необходимо прежде всего сформулировать критерий качества распознавания. Решающее правило должно быть выбрано таким образом, чтобы сформулированный критерий достигал экстремума.

Предположим, что ситуация Х появляется случайно и каждая из возникающих ситуаций принадлежит к одному из m неизвестных ранее классов Q_i(i=1,…,m).

Обозначим через Х пространство ситуаций и разобьем его на m областей. Задача распознавания состоит в наилучшем разбиении пространства Х на области Q_i. Чтобы конкретизировать это понятие, введем функцию потерь:

F_i(X, ), i=1,..,m,

где = (C₁,…,C_m) – составной вектор параметров.

Функции потерь характеризуют потери, возникающие при отнесении ситуации класса Q⁰_i к классу Q⁰_k или, иначе, при попадании ситуации класса Q⁰_i в область Q⁰_k.

Функции потерь образуют платежную матрицу:

F₁₁(x, ) F₁₂(x, ) … F_1m(x, )

F₂₁(x, ) F₂₂(x, ) … F_2m(x, )

F_m1(x, ) F_m2(x, ) … F_mm(x, )

По главной диагонали матрицы расположены потери при правильных решениях, а по обеим сторонам от главной диагонали – потери при ошибочных решениях.

Если F_mm(x, )<0, то такие отрицательные потери можно рассматривать как выигрыши при правильном решении.

Ситуация Х каждого класса Q_i характеризуется условной плотностью распределения P(x/Q_i) = P_i(X) и априорной вероятностью P(Q_i). Потому качество распознавания можно оценивать средним риском:

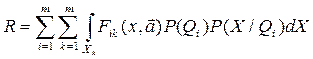
Средний риск в нашем случае представляет собой функционал границ L_ik между областями X_i и X_k и составного вектора .

P(X/Q_i) P(Q_i)

X

X

Рис. Формирование решающего правила

Особенность R: здесь функции потерь не постоянны, а зависят от ситуаций х и составного вектора параметров .

С этих позиций цель обучения:

- P(Q_i) – неизвестно; P(X/Q_i) – неизвестно;

- единственно, чем располагаем – то платежной матрицей, элементы

которой заданы с точностью до некоторых неизвестных векторных параметров .

Тогда цель: минимум неявно заданного среднего риска:

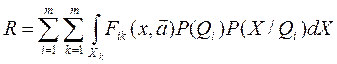
Начальный этап обучения характеризуется поиском алгоритмов оценки параметров {а}.

Определение: Задача оценки параметров, относящаяся к классическим задачам математической статистики, может быть решена различными способами. Рассмотрим два из них:

а) оценку по максимуму правдоподобия, при этом: значения параметров предполагаются фиксированными, но неизвестными.

При обучении с учителем известен индекс класса для каждого P(Q_i)

Общая идея метода

Предположим, что множество выборки разбито на классы, так что получено m классов выборок Q₁,…,Q_m, выборки X₁,…,X_m для каждого класса получены независимо и в соответствии с вероятностью P(X/Q_i). Предполагается, что плотность P(X/Q_i) задана в известной параметрической форме, и, следовательно, однозначно определяется вектором параметров . Можно получить, например, распределение P(X/Q_i)~N(m_i,å_I), в котором компоненты a_i составлены из компонент m_i и K_i. Тогда P(X/Q_i) запишем как P(X/Q_i,a_i).

Задача состоит в использовании информации, получаемой из выборки, для удовлетворительной оценки векторов параметров {a_i}. Для облегчения задачи предположим, что выборки, принадлежащие X_j, не содержат информации об a_i, i¹j, т.е. предполагается функциональная независимость параметров, принадлежащих разным классам {Q_i}.

В результате получается i отдельных задач, формулируемых следующим образом: на основании множества {X} независимо полученных выборок в соответствии с вероятностным законом P(X/a) оценить неизвестный параметрический вектор .

Предположим, что Х содержит n выборок: X = {x₁,…,x_n}, т.к. выборки получены независимо, имеем:

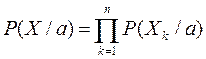
где P(X/a) – правдоподобие величины а относительно данного множества выборок.

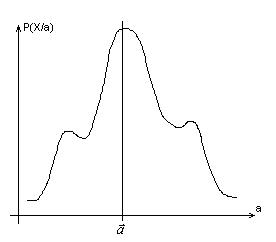
Определение: Оценка по максимуму правдоподобия величины а есть такая , при которой P(X/a) максимальна.

Интуитивно это означает, что в некотором смысле такое значение величины а наилучшим образом соответствует реально наблюдаемым выборкам.

Для анализа удобнее использовать логарифм правдоподобия как монотонно возрастающую функцию, т.е. максимуму логарифма и максимуму правдоподобия соответствует одна и та же величина .

Если P(X/a) есть гладкая дифференцируемая функция а, то определяется посредством обычных методов дифференциального исчисления.

Пусть есть р – компонентный вектор = (а₁,…,а_р)^Т, пусть Ñа – оператор градиента. Т.е.

Ñа = ,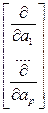

и пусть 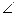(а) – функция логарифма правдоподобия.

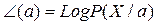, т.е.

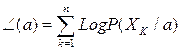
и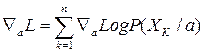

Совокупность условий, необходимых для определения оценки по максимуму правдоподобия величины а, может быть получена, т.о. из решения системы р уравнений Ñ_аL=0:

Ñ_аL=0 для одного а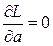

Случай многомерного N(m,s) при неизвестном m:

При том:

1)

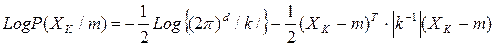
2)

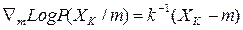
где к - ковариационная матрица.

Если отождествлять m и “a”, то оценка по максимуму правдоподобия для m должна удовлетворять уравнению:

После умножения на к и преобразования получим:

Этот результат весьма убедителен. Он свидетельствует о том, что оценки по максимуму правдоподобия при неизвестном среднем по совокупности в точности рана среднему арифметическому выборок – выборочному среднему.

Если представить “И” выборок, то выборочное среднее будет центром этого облака.

Таким образом, и в случае обучения по методу максимума правдоподобия неизвестное среднее (математическое ожидание) находится как выборочное среднее – максимально правдоподобное решение.

Случай многомерного N(m,s), когда неизвестны ни m, ни s. Эти неизвестные параметры образуют компоненты параметрического вектора .

Рассмотрим одномерный случай, приняв a₁=m и a₂=s². Тогда имеем:

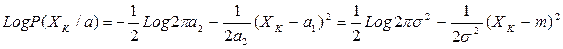
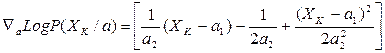
Тогда получим:

и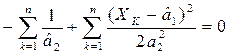

где 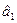и 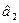- оценки по максимуму правдоподобия соответствуют а₁ и а₂. После подстановки получим:

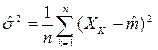
Для многомерного случая соответственно имеем:

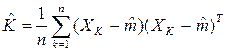
Следствие: Таким образом, оценка по максимальному правдоподобию для среднего значения вектора – то выборочное среднее. А оценка по максимальному правдоподобию для ковариационной матрицы – это среднее арифметическое n матриц 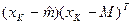т.к. подлинная ковариационная матрица и есть ожидаемое значение матрицы (x-m)(x-m)^T, то полученный результат также весьма естественен.

б) метод Байесовской классификации.

Несмотря на то, что результаты по Байесу и методу максимального правдоподобия оказываются весьма близкими, подход к решению по критерию Байеса различен (сильно отличаются).

Здесь параметры рассматриваются как случайные переменные с некоторым априорно заданным распределением. Исходя из результатов распределения выборок, это распределение преобразуют в апостериорную плотность, используемую для уточнения имеющегося представления об истинных значениях параметров.

В байесовском случае характерным следствием привлечения добавочных выборок является заострение формы функции апостериорной плотности, подъем ее вблизи истинных значений параметров. Это явление принято называть байесовским обучением.

Определение: Сущность байесовской классификации заложена в расчете апостериорных вероятностей P(Q_i/X). Байесовское правило позволяет вычислить эти вероятности по априорным вероятностям P(Q_i) и условным по классу распределениям P(X/Q_i). Однако, как быть, если эти величины неизвестны?

Общий ответ: Лучшее, что можно сделать – то вычислить P(Q_i/X), используя всю информацию, имеющеюся в распоряжении.

Часть информации – априорная, часть информации – в выборках.

Пусть имеется множество выборок {X}, тогда вычисляются апостериорные вероятности P(Q_i/x,X). По этим вероятностям мы можем построить байесовский классификатор.

Согласно байесовскому правилу:

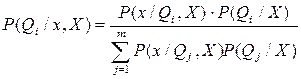
Это выражение означает, что мы можем использовать информацию, получаемую из выборок, для определения как условных по классу распределений, так и априорных вероятностей. Впредь полагаем, что истинные значения априорных вероятностей известны, так что P(Q_i/X) = P(Q_i). Кроме того, т.к. в данном случае мы имеем дело с наблюдаемыми значениями, то можно разделить выборки по классам в подмножеств x₁,…,x_m, причем выборки из X_i принадлежат Q_i. Выборки из X_i не оказывают влияния на P(X/Q_i,X), если i¹j. Отсюда вытекают два следствия:

1) можно иметь дело с каждым классом в отдельности, используя для

определения P(x/Q_i,X) только выборки из X_i. Вместе с тем, что априорные вероятности известны, то следствие позволяет записать:

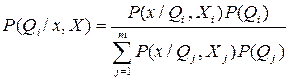
2) так как каждый класс может рассматриваться независимо, можно

отказаться от ненужных различий классов. По существу, здесь имеется m отдельных задач вида: требуется определить P(x/X), используя множество Х выборок, взятых независимо в соответствии с фиксированным, но неизвестным Р(Х). Это и составляет главную задачу байесовского обучения.

Предпосылка 1: Р(Х) неизвестно, но имеет известный параметрический вид. Выразим это утверждением что функция Р(Х/а) полностью известна.

Предпосылка 2: При байесовском подходе предполагается, что всю информацию до наблюдения выборок дает известная априорная плотность Р(а). Наблюдение выборок превращает ее в апостериорную плотность Р(а/х), которая, как можно предположить, имеет крутой подъем вблизи истинного “a”.

Обучение без учителя (самообучение)

До сих пор мы предполагали, что обучающие выборки, используемые для распознавания, были помечены, чтобы показать, к какой категории они принадлежат. Это – обучение с учителем.

Пусть имеется набор непомеченных выборок. Имеются три основных причины необходимости самообучения (работы с непомеченными выборками).

1) сбор и мечение большого количества выборочных образов требует

много средств и времени;

2) во многих практических задачах характеристики образов медленно

меняются во времени;

3) на ранних этапах исследования иногда бывает интересно получить

сведения о внутренней природе или структуре данных.

Первое предположение: пусть функциональный вид плотностей распределения известен, и, единственное, что надо узнать, то значение вектора неизвестных параметров. Формальное решение этой задачи оказывается почти идентичным задаче с учителем. Задача формулируется следующим образом:

1. Выборки производятся из известного числа m классов;

2. Априорные вероятности P(Q_i) для каждого класса известны, i=1,2,…,m.

3. Вид условных по классам плотностей P(x/Q_i,a) известен, i=1,…,m.

4. Единственное неизвестное – это значения m параметрических векторов a₁,…,a_m.

Предполагается, что выборки получены выделением состояния природы

Q_i с вероятностью P(Q_i) и последующим выделением Х в соответствии с вероятностным законом P(x/Q_i,a). Таким образом, функция плотности распределения выборок определяется как:

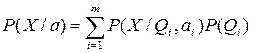
Р(Х/а) – плотность смеси. Условные плотности P(X/Q_i,a_i) называются плотностями компонент, а априорные вероятности P(Q_i) – параметрами смеси.

Если мы знаем а, то можем разложить смесь на компоненты и задача решена. Однако, если несколько различных значений а могут дать одни и те же значения для Р(Х/а), то нет надежды получить единственное решение.

Эти рассмотрения приводят нам к следующему определению:

Определение: Плотность Р(Х/а) считается идентифицируемой, если а¹а^/ следует, что существует х такой, что Р(х/а)¹Р(х/а^/). Таким образом, самообучение значительно упрощается, если мы ограничиваемся идентифицируемыми смесями.

Для нормальной плотности:

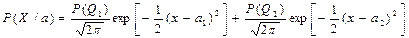
Идентификация смеси имеет место, если P(Q₁)¹P(Q₂).