Последовательный анализ

Отличительной особенностью всех рассмотренных процедур выбора решения при распознавании (проверка простой гипотезы) была неизменность заранее заданного размера выборки n.

Наряду с этим существует другой подход к установлению правила выбора решения, при котором отказываются от постоянного размера выборки, а ограничивают эту величину в процессе эксперимента в зависимости от результатов уже выполненных наблюдений.

Алгоритм последовательного анализа:

1) вначале наблюдают первое значение х1 (т.е. извлекают выборку значения n=1);

2) выбирают одно из 3-х решений:

– принять гипотезу H₀ (решение g₀);

– принять гипотезу Н₁ (решение g₁);

– продолжить наблюдения, т.е. отказаться от принятия решений g₀ и g₁.

3) при принятии решений эксперименты заканчиваются;

4) в противном случае извлекают следующую выборку (х1,х2,n=2) (процедуры повторяются);

5) если окончательное решение не принято, то извлекается новая выборка и т.д.;

6) испытание заканчивается на той выборке, на основании которой принимается решение g₀ и g₁.

Определение: При последовательном анализе размер выборки заранее

неизвестен и является случайной величиной.

На каждом этапе пространство выборки делится на 3 области (а не на две!):

- G₁ – критическую;

- G₀ – допустимую;

- G_ПР – промежуточную.

Тогда алгоритм:

- если очередное X_i попадает в критическую область G₁, то гипотеза H₀ отвергается;

- если X_i попадает в допустимую область G₀, то она принимается;

- если выборочное значение попало в промежуточную область G_ПР, то наблюдения продолжаются.

Следствие: Поскольку число способов разбиения пространства выбора

в принципе не ограничено, то неизбежен набор различных правил выбора решения. Тогда необходимо формирование критериев качества, с помощью которых можно сравнивать различные процедуры последовательного анализа и выбрать наилучшую.

Критерии качества

1. минимальная средняя стоимость эксперимента.

Определение: Если считать, что стоимость эксперимента пропорциональна размеру выборки n, то критерием качества последовательного правила выбора решения является минимум среднего значения размера выборки n, необходимый для принятия решений g₀ и g₁ при условии, что уровень значимость не превышает a!!, а мощность – не меньше, чем 1-b!!.

Следствие: Среднее значение размера выборки m₁(n/H₀) и m₁(n/H₁) при справедливости гипотез Н₀ и Н₁, соответственно, в общем случае не равны и требуется минимизация обеих величин.

Правило Вальда

Для всех правил выборки решения, где условные вероятности ошибок a и b не превосходят заданных значений, последовательное правило, состоящее в сравнении отношения правдоподобия L(x₁,…,x_n) с двумя порогами С₀ и С₁, приводит к наименьшим затратам (значениям) m₁(n/H₀) и m₁(n/H₁).

Оптимальное разбиение пространства выборки определяется неравенствами:

1) для допустимой области G₀:

C₀ < L(x₁,…,x_k) < C₁; k=1,…,n-1; L(x₁,…,x_n) 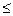C₀;

2) для критической области G₁:

C₀ < L(x₁,…,x_k) < C₁; k=1,…,n-1; L(x₁,…,x_n) 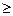C₁;

3) для промежуточной области G_ПР:

C₀ < L(x₁,…,x_n) < C₁; k=1,…,n.

Точное определение С₀ и С₁ математически сложно. Однако, доказано, что:

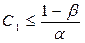
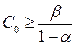
Пример: Проверка простой гипотезы о параметрическом распределении:

- гипотеза Н₀: среднее значение нормальной случайной величины равно а₀;

- альтернативная гипотеза Н₁: среднее значение нормальной случайной величины а₁.

Тогда N(s,a₀) или N(s,a₁)?

Элементы х1,…,х_n – независимы.

Пусть имеем пока один порог С₁, с которым сравнивается L(x) или

LnL(x). Для нормального закона:

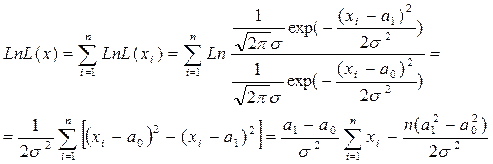
При фиксированном размере выборки имеем правило g₁:

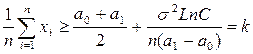а₁>a₀

Для критерия максимального правдоподобия:

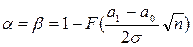
Замечательное следствие: При заданном a=b из этой формулы находим необходимый размер выборки:

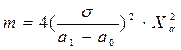
где Х²_a = argF(X).

В математической статистике Xa называют процентным отклонением случайной величины, т.е. такую абсциссу кривой распределения, которая характеризуется тем, что часть площади под этой кривой находящаяся правее Хa, равна Х.

т.е. P{x 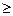X_a} = a.

Для критерия Неймана – Пирсона на заданном уровне значимости a величина К определяется по формуле (а₁>а₀):

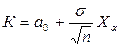
Еще одно следствие: Вероятности ошибок a и b в байесовском решении и вероятность ошибки 2-го рода для критерия Неймана – Пирсона зависят не от каждой из величин n, а₁, а₀, s в отдельности, а лишь от их единственной комбинации 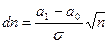. Отсюда следует, что при уменьшении величины 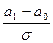(в к раз, случай различения близких гипотез) для сохранения величин вероятности ошибок потребуется увеличение (в к² раз!) размера выборки n.

Если а₁<а₀, то решение g₁ по критерию Неймана - Пирсона принимается при условии, что:

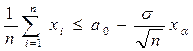
Ситуация 2: Вид аналитической функции априори неизвестен, т.е. характер априорной неопределенности таков, что какие-либо сведения об аналитическом описании исходного материала полностью отсутствуют: неизвестно распределение вероятности наблюдаемых значений x_i, i=1,…,n, неизвестен вид платежной матрицы (функции потерь), неизвестны также плотности вероятности параметров f(a_x), влияющих на величину потерь, неизвестны и последствия от принятия того или иного решения (виды оценивания).

За ту крайность приходится расплачиваться довольно серьезными ограничениями, которые выражают иную форму представления имеющихся априорных значений, отличную от параметрических описаний.

Следствие: Таким образом, параметрическое и непараметрическое описания исходных данных задачи соответствуют разным видам имеющихся ограниченных априорных знаний и взаимно дополняют друг друга.