Глава 5. РАСПОЗНАВАНИЕ И КЛАССИФИКАЦИЯ ОБРАЗОВ НА ОСНОВЕ ИСПОЛЬЗОВАНИЯ ПРЕДПОЛОЖЕНИЯ О БЛИЗОСТИ ОПИСАНИЙ
При решении задач распознавания и классификации с использованием предположения о близости описаний, оценивается среднее расстояние между описаниями неизвестного объекта и каждого объекта из известного множества,т. е. предполагается усреднение по измерениям для объектов из этого множества [1]. По сравнению с классическим подходом эти методы классификации основаны на более слабом предположении, что объекты, описания которых расположены близко друг от друга в
m-мерном пространстве описаний D, могут принадлежать одному и тому же классу. Например, пол конкретного человека обычно определяют, выясняя его схожесть с произвольно выбранным мужчиной или с женщиной. Другой пример – происхождение классической греческой скульптуры или мраморной кладки устанавливается по оценкам относительного количества различных изотопов химических элементов в мраморе. Обнаружено, что мрамор из античных карьеров можно отличать по отношению концентраций углерода-13 к углероду-12 и кислорода-18 к кислороду-16. Разумеется, необходимы надежно обоснованные правила отнесения каждого из исследуемых фрагментов скульптуры или кладки к соответствующему карьеру.
Объект с описанием x похож на объекты с описаниями, принадлежащими некоторому множеству  , если мало среднее значение квадрата расстояния между точками x и точками множества Y =
, если мало среднее значение квадрата расстояния между точками x и точками множества Y =  .
.
При сравнении двух множеств оценивается среднее расстояние между двумя точками, взятыми по одной из каждого множества. Для множеств X и Y, содержащих соответственно 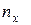 и
и 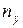 точек, среднеквадратичное значение расстояния между X и Y равно
точек, среднеквадратичное значение расстояния между X и Y равно

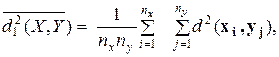 (27)
(27)
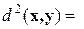
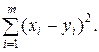
Чем дальше в среднем друг от друга точки из X и Y, тем больше значение 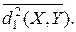 Плотность расположения точек внутри множества обычно оценивается среднеквадратичным значением расстояния между точками этого множества:
Плотность расположения точек внутри множества обычно оценивается среднеквадратичным значением расстояния между точками этого множества:
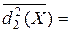
 (28)
(28)
Классификация, основанная на близости описаний, заключается в преобразовании пространства описаний D в пространство D*, в котором все точки одного множества расположены близко друг к другу, а точки различных – удалены на некоторое расстояние. Пространство D* формируется в результате линейного преобразования m-мерного пространства D, когда каждая точка x Î D отображается в точку x* Î D* по формуле
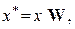
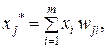 (29)
(29)
где W – симметричная (m 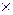 m)-матрица, wji – элементы матрицы.
m)-матрица, wji – элементы матрицы.
ВАРИАНТЫ РЕАЛИЗАЦИИ МЕТОДА КЛАССИФИКАЦИИ, ОСНОВАННОГО НА БЛИЗОСТИ ОПИСАНИЙ
Метод классификации, в котором для установления сходства объектов в пределах одного множества пространство описаний 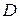 трансформируется с целью минимизации среднеквадратичного расстояния
трансформируется с целью минимизации среднеквадратичного расстояния 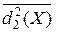 между двумя точками, требует для каждого класса отдельного преобразования, что усложняет весь процесс классификации. Другой недостаток заключается в том, что изучение каждого класса в отдельности не позволяет обнаруживать степень различия между классами в пространстве исходных измерений.
между двумя точками, требует для каждого класса отдельного преобразования, что усложняет весь процесс классификации. Другой недостаток заключается в том, что изучение каждого класса в отдельности не позволяет обнаруживать степень различия между классами в пространстве исходных измерений.
Отмеченные недостатки устраняются при использовании дискриминантного критерия. Он состоит в максимизации различия между точками разных множеств; при этом сумма расстояний между точками внутри и между множествами остается постоянной. Этот подход приводит к единой составной мере, по которой местоположения точек одного множества близки, а разных множеств существенно отличаются.
В качестве геометрической интерпретации составной меры можно представить себе прямую линию в m-мерном пространстве, выходящую из начала координат пространства D. Пространственное положение этой линии выбирается таким образом, чтобы точки одного множества проектировались в одну и ту же ее область, а разных множеств – в разные области. Эффективность такого подхода можно проиллюстрировать результатами его использования при решении упомянутой ранее задачи классификации – установлении происхождения материала археологических мраморных обломов при помощи изотопов. На рис. 12 приведены результаты измерений, полученные для образцов из различных карьеров. Данные, определяющие оси, выведены из отношений 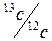 и
и 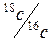 с помощью сложных расчетов, в которых измерения исследуемого фрагмента сопоставлялись с аналогичными измерениями для стандартных образцов.
с помощью сложных расчетов, в которых измерения исследуемого фрагмента сопоставлялись с аналогичными измерениями для стандартных образцов.
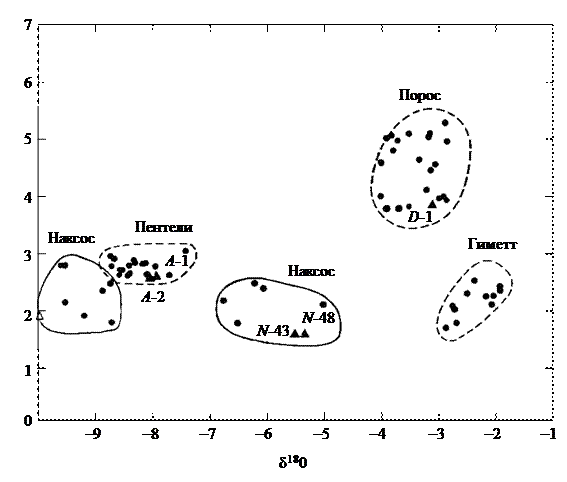
Рис. 12. Отклонения содержания углерода-13 и кислорода-18 (относительно
стандарта PDP) в образцах мрамора из античных карьеров.
Треугольниками обозначены мраморные обломы (Крейг, 1972).
Наименования обломов: А-1 (наименование происхождения – Пентели),
А-2 (наименование происхождения – неизвестно); D-1 (Парос);
N-43 (Наксос), N-48 (Наксос)
Точки, соответствующие множествам образцов из карьеров Парос, Гиметт и Пентели, спроектированные на ось L, изображены на рис. 13. Прямая L – это составная мера, которая определяется взвешенными суммами упомянутых выше отношений кислорода и углерода.
Соответствующие вычислительные процедуры используют три вспомогательные матрицы G, V и T. Для любой пары точек x, y Î D
определим матрицу G(x,y) порядка m с элементами
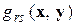 =
=  (x, y). (30)
(x, y). (30)

Рис. 13. Проекции на соответствующие оптимальные собственные векторы
Предположим, что исходные данные состоят из k множеств X1, …, Xk наблюдений, соответствующих k классам. Обозначим через 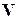 усредненную матрицу G(x,y) по всем парам точек x и y из различных множеств
усредненную матрицу G(x,y) по всем парам точек x и y из различных множеств
Xi и Xj, а через 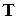 – усредненную матрицу G(x,y) по всем парам независимо от принадлежности их какому-то классу. Алгебраически это можно записать следующим образом:
– усредненную матрицу G(x,y) по всем парам независимо от принадлежности их какому-то классу. Алгебраически это можно записать следующим образом:
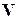 =
= 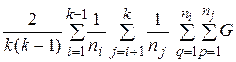 (x
(x 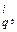 y
y 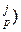 , (31)
, (31)
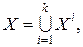
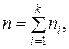
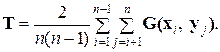 (32)
(32)
Для дальнейших рассуждений необходимо напомнить, как определяются собственные векторы и собственные значения матрицы. Рассмотрим для заданной квадратной матрицы 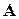 порядка n следующее уравнение
порядка n следующее уравнение
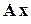 =
= 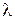
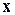 , (33)
, (33)
где 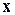 – неизвестный числовой вектор, высота которого равна порядку матрицы
– неизвестный числовой вектор, высота которого равна порядку матрицы 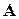 , а
, а 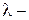 неизвестное число. Данное уравнение при любом
неизвестное число. Данное уравнение при любом 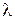 обладает тривиальным решением
обладает тривиальным решением 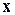 = 0. Однако нас интересуют только такие значения
= 0. Однако нас интересуют только такие значения 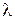 , при которых эта система имеет нетривиальные решения. Эти значения
, при которых эта система имеет нетривиальные решения. Эти значения 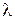 называются собственными значениями матрицы
называются собственными значениями матрицы 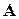 , а решения
, а решения 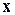 данного уравнения при этих
данного уравнения при этих 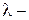 ее собственными векторами.
ее собственными векторами.
Собственные значения и собственные векторы находятся следующим образом. Поскольку x =Ix, где I – единичная диагональная матрица, то можно записать
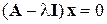 , (34)
, (34)
т. е. мы имеем дело с системой из n алгебраических линейных однородных (без свободных членов) уравнений с n неизвестными, где n – порядок матрицы А. Для наличия нетривиального решения необходимо и достаточно, чтобы определитель системы равнялся нулю, т. е.
│A – λI│= 0. (35)
Это уравнение называется характеристическим уравнением матрицы 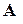 ,оно служит для определения собственных векторов и собственных значений
,оно служит для определения собственных векторов и собственных значений 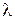 . Так, для матрицы
. Так, для матрицы
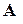
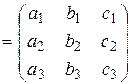 (36)
(36)
характеристическое уравнение имеет вид
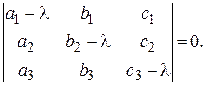 (37)
(37)
При раскрытии определителя получаем алгебраическое уравнение, степень которого равна порядку матрицы A, т. е. матрица порядка n имеет n собственных значений, среди которых, правда, могут быть совпадающие.
Зная собственные значения, можно найти соответствующие собственные векторы из векторного уравнения (34), переписанного в виде системы скалярных уравнений
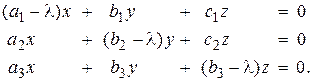 (38)
(38)
Определим матрицу  , строки которой являются собственными векторами матрицы VT-1 (T-1 – матрица, обратная для матрицы T, T-1T = I).
, строки которой являются собственными векторами матрицы VT-1 (T-1 – матрица, обратная для матрицы T, T-1T = I).
Тогда W1 – собственный вектор, соответствующий наибольшему собственному значению 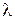 . Для определения обратной матрицы T-1 необходимо знать следующее правило:
. Для определения обратной матрицы T-1 необходимо знать следующее правило:
если  (39)
(39)
то  (40)
(40)
где большими буквами A1, …, C3 обозначены алгебраические дополнения соответствующих элементов в матрице T.
Собственный вектор W1 определяетнаправление прямой L, выходящей из начала координат пространства D и максимально разделяющей точки различных множеств. Прямая линия L образует с j-й осью dj  пространства D угол, такой, что
пространства D угол, такой, что
cos(L, dj) = w1, j (41)
Определением прямой L завершается этап распознавания образов. На этапе классификации объект относится к классу i в зависимости от положения на прямой L проекции его описания y. Для любой точки
x Î D обозначим
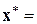
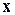
 (42)
(42)
Вектор 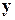 из класса i = 1, …, k классифицируется как описание объекта тогда и только тогда, когда величина
из класса i = 1, …, k классифицируется как описание объекта тогда и только тогда, когда величина
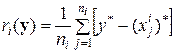 (43)
(43)
минимальна.
Недостаток дискриминантногометода состоит в том, что, хотя он приводит к хорошей мере для классификации по всем классам, он не обязательно дает хорошую меру для каждого класса в отдельности. Как видно на рис. 12, ни одна прямая не может разделить все классы, поскольку наилучшая прямая для разделения множеств Пентели и Наксос ориентирована не так, как оптимальная прямая, разделяющая все множества за исключением Наксос.
| <== предыдущая лекция | | | следующая лекция ==> |
| ПАРАЛЛЕЛЬНАЯ ПРОЦЕДУРА КЛАССИФИКАЦИИ ОБРАЗОВ НА ОСНОВЕ БАЙЕСОВСКОЙ ОЦЕНКИ ВЕРОЯТНОСТЕЙ ОСУЩЕСТВЛЕНИЯ РАЗЛИЧНЫХ ГИПОТЕЗ | | | Алгоритм коррекции по ошибкам для двух классов |
Дата добавления: 2016-01-20; просмотров: 803;
