ПАРАЛЛЕЛЬНАЯ ПРОЦЕДУРА КЛАССИФИКАЦИИ ОБРАЗОВ НА ОСНОВЕ БАЙЕСОВСКОЙ ОЦЕНКИ ВЕРОЯТНОСТЕЙ ОСУЩЕСТВЛЕНИЯ РАЗЛИЧНЫХ ГИПОТЕЗ

Особенность параллельной реализации байесовского правила классификации состоит в том, что роль гипотез здесь принадлежит названию классов, а описание классифицируемого объекта – совокупность xизмерений параметров объекта – выполняет функции экспериментального наблюдения. Каждый классифицируемый объект соответствует точно одному классу, при этом два различных объекта из двух разных классов могут дать одинаковые векторы описания.

Пусть наблюдается объект с описанием x, а j – событие «классифицируемый объект принадлежит классу j». Устройство классификации образов должно относить объект с описанием x к классу «j» только при выполнении следующего неравенства:

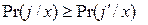для всех .

Пространство описаний D разбивается на такие области {R_j}, что это выражение удовлетворяется для всех точек из области {R_j} и только для них. Затем объекты классифицируются в соответствии с областью, в которую попадает x.

В качестве примера представим, что необходимо в какой-то компании обследовать всех служащих, у которых врачи наблюдали признаки серьезных психических отклонений. О тщательном обследовании каждого служащего в отдельности для большой компании не может быть и речи. Разумной альтернативой является целевой анкетный персональный тест, а затем обследование тех, чьи результаты выглядят подозрительно.

В данной задаче распознавания образов служащие являются классифицируемыми объектами, а очки, полученные в тестах, образуют
одномерное пространство описаний. Допустим, что в предыдущем обследовании для лиц с психическими отклонениями установлено нормальное распределение тестовых очков со средним значением 130 и среднеквадратичным отклонением 10, а для психически здоровых людей указанные параметры этого распределения оказались равными соответственно 110 и 20 (рис. 10).

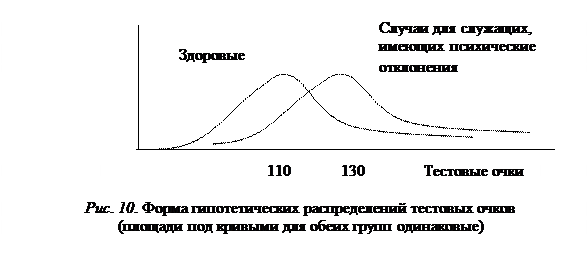
Представленные на рис. 10 примерные кривые распределений показывают, с одной стороны, возможность с помощью данного теста различать две упомянутые группы служащих, а с другой стороны – наличие определенных сложностей в реализации данной процедуры, обусловленных частичным перекрытием этих распределений. Кроме того, чтобы применить правило классификации, надо учесть, что здоровых людей, скажем, в 10 раз больше, чем людей с психическими отклонениями. Это означает, что площадь под кривой на рис. 10, соответствующей распределению для случаев психических отклонений, должна составлять 0,1 от площади под кривой распределения для здоровых людей, но форма первой остается прежней (рис.

Ответ на вопрос, какова область тестовых измерений, в которой абсолютное количество случаев психических отклонений превышает абсолютное количество здоровых, очевиден из анализа рис. 11. «Психически ненадежными» служащие могут считаться (и, следовательно, должны быть подвергнуты дополнительному обследованию) только в том случае, если их очки превышают отмеченное на рисунке критическое значение 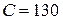, т. е. «наиболее типичного результата» для психически больных.

При такой минимизации общего количества неверных классификаций больше половины психически больных служащих будут классифицироваться как здоровые. Полученный сопутствующий результат непосредственно вытекает из формулы Байеса

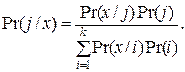(24)

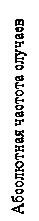
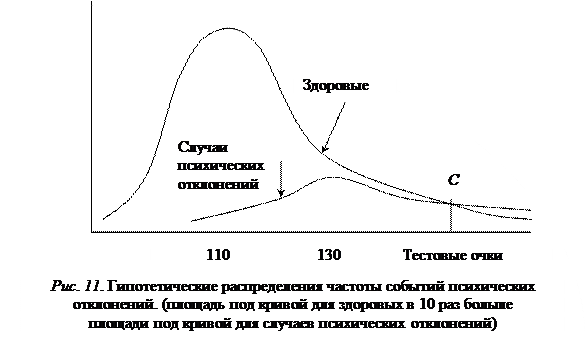
Зависимость байесовского правила оценки вероятности гипотез (24) от условной вероятности Pr(x/i) и от априорных вероятностей Pr(i) для класса «i» в рассмотренном примере не учитывает относительных стоимостей ошибочных классификаций. В рассматриваемом случае более серьезной ошибкой будет не обследовать психически ненадежного человека, чем потратить время на обследование людей без очевидных психических отклонений.

Простой способ учета таких соображений при байесовской классификации состоит в следующем. Обозначим c(i/j) цену неправильного отнесения при классификации точки x класса j к классу i, тогда ожидаемые потери из-за ошибочной классификации точки x равны

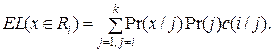(25)

Чтобы минимизировать ожидаемые потери 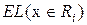из-за ошибочной классификации по всем точкам пространства D, границы между двумя соседними областями R_i и R_j задаются уравнением

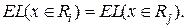(26)

Исследование формы этой границы может быть полезным для неформального понимания существа процедуры классификации.