БАЙЕСОВСКОЕ ПРАВИЛО

Байесовский метод классификации образов рассматривается как частный случай решения более общей задачи выбора одного из возможных объяснений на основе имеющихся данных. Он используется в качестве нормативной модели того, как следует себя вести в подобных случаях, а также для описания процессов, происходящих на самом деле. В задачах параллельной евклидовой классификации широко используемая следующая процедура.

Пусть A и B – дискретные события, которые характеризуются следующими вероятностями появления:

Pr(A) – вероятность появления события А;

Pr(В/А) – вероятность (условная вероятность) появления события В при условии наличия события A;

Pr(A, B) = Pr(A) Pr(В/А) – вероятность совместного появления событий
А и В.

В байесовской задаче исходное множество гипотез H = 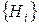определяет все возможные «состояния мира», которые исключают друг друга, поскольку мир должен находиться только в одном из состояний. С каждой гипотезой H_iсвязана (субъективная) вероятность Pr(H_i) того, что она на самом деле выполняется. Отсюда следует, что Pr(H_i, H_j) = 0 (взаимно исключающие события), 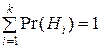(полнота).

Прямым наблюдением нельзя проверить, истинна гипотеза H_i или нет; в ходе эксперимента получают множество E = {E_j}, j = 1, …, n, наблюдаемых исходов. Поскольку в каждом отдельном эксперименте имеет место только один исход, события E_j взаимоисключающие. Итак, имеют место следующие определения:

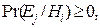
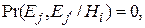
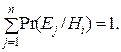
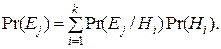
В рассматриваемом далее конкретном примере гипотезы состоят в том, что дождь идет или не идет , а эксперимент заключается в наблюдении следующих возможных событий за окном:

(а) на улице нет людей;

(б) как минимум у одного человека на улице есть зонтик;

(в) на улице есть люди, но ни у кого из них нет зонтика.

Представим себе пасмурный осенний день, для которого априорные вероятности того, идет дождь или нет, примем табл. 7:

Таблица 7

Обозначение	Пояснение	Величина
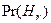
	Вероятность того, что идет дождь	0,3
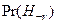
	Вероятность того, что дождь не идет	0,7

Если идет дождь, то более вероятно, что улица пуста, а если кто-то должен выйти на улицу, то он, вероятнее всего, возьмет зонтик (табл. 8).

Таблица 8

Обоснование	Пояснение	Величина
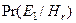
	Дождь, у людей на улице не менее одного зонтика	0,4
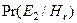
	Дождь, все люди на улице без зонтиков	0,2
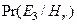
	Дождь, улица пуста	0,4
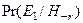
	Нет дождя, у людей на улице не менее одного зонтика	0,05
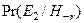
	Нет дождя, ни у кого на улице нет зонтика	0,75
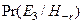
	Нет дождя, улица пуста	0,2

Одной из задач может быть следующая: мы видим человека с зонтиком, какова вероятность того, что идет дождь? Задача состоит в вычислении вероятности 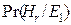того, что идет дождь при условии, что на улице есть человек с зонтиком. Примем следующие значения условных плотностей вероятностей.

Используя определение совместной вероятности, получаем

,

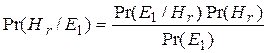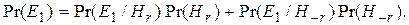
В итоге байесовское правило оценки вероятности осуществления гипотезы на основе наблюдаемых событий выглядит следующим образом

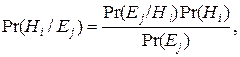
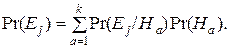
Это правило применимо, если существует фиксированное множество гипотез и для каждой из них известны вероятности различных наблюдений. Оно применимо как для параллельных, так и для последовательных процедур распознавания образов.