Главный вектор и главный момент системы сил. Правило Пуансо.

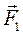Пусть заданы какие-то два произвольных вектора и 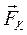. Мы хотим сложить эти два вектора. Если что-то складывать, то, во-первых, надо выбрать место, куда складывать, а во-вторых, определиться, как складывать. "Место'"— это центр приведения, выбранная нами произвольно точка О. А правила сложения объяс­ним на конкретном примере. Приложим нулевой вектор ( 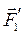, 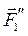) в точке О, причем выберем модули этих векторов равными модулю 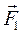. Итак, был вектор 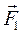, стала совокупность трёх векторов ( 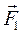, , 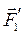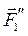)). Сгруппируем их теперь по другому( 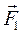, ( , 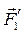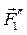))≈( 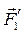,( ,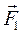, 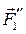)). Вроде бы ничего не изменилось (знак ≈ обозначает эквивалентность), но получили силу 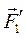,приложенную в выбранном центре О, и совокупность ( 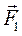, 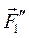), образующих пару сил с моментом 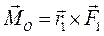. Если проделать те же операции с вектором 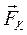, то получим

≈( ,( , ))≈( ,( , ))

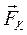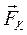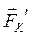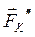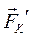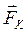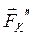то-есть получили силу 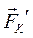, приложенную в выбранном центре, и пару сил ( 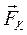, 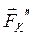) с моментом 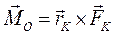.Теперь два вектора приложены в том же центре О, и их можно сложить по правилу параллелограмма. Но!!! Помимо суммы этих двух векторов еще есть сумма двух пар, двух свободных векторов, которое тоже можно сложить и получить результирующий вектор момента. Получили СИЛУ и МОМЕНТ! Чему равна сила? — сумме двух заданных сил. а момент? - моменту этих двух сил относительно выбранно­го центра. Все изложенные соображения можно распространить и на сколь угодное количество сил. Результатом этих преобразований будет сила, равная сумме слагаемых сил, и пара сил с моментом равным сумме моментов пар.

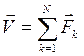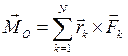, ( 1.3 )

Вектор 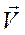называется – главный вектор системы сил.

Вектор 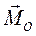называется – главный момент системы сил относительно выбранного центра.

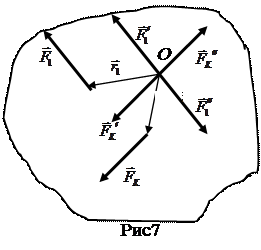
Метод Пуансо приводит, таким образом, к следующей основной теореме статики: произвольная пространственная система сил, приложенная к твердому телу, статически эквивалентна силе, равной главному вектору, приложенной в произвольной точке тела (центре приведения), и паре сил с моментом, равным главному моменту системы сил относительно указанного центра приведения.

Теперь можно дать более точную формулировку статической эквивалентности двух систем сил: если две системы сил имеют одинаковые главные векторы и главные моменты относительно одного и того же центра приведения, то такие системы сил статически эквивалентны.

Как меняются главный вектор и главный момент при переходе к другому центру приведения? Из построения на рис. 7 видно, что сумма всех сил, а, следовательно, и главный вектор системы сил, не изменится. Главный же момент будет другой, так как теперь моменты сил надо будет считать относительно другого центра, плечи пар станут другими. Пусть новый центр будет в точке Р. Тогда,

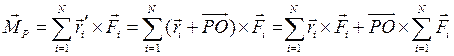(5)

Первое слагаемое - момент сил относительно старого цен­тра, второе- момент главного вектора относительно нового центра, тогда окончательно запишем

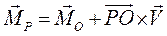(1.4) т.е. главный момент сил зависит от центра приведения. Умножим скалярно выражение (1.4) на орт главного вектор, т.е. спроектируем вектор главного момента на направление главного вектора сил

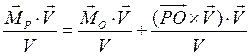
Второе слагаемое равно нулю как скалярное произведение ортогональных векторов, следовательно

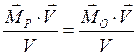(1.5)

Проекция главного момента на направление главного вектора есть величина постоянная и не зависит от выбора центра приведения. Величины, не зависящие от выбора центра приведения, называются статическими инвариантами. Т.о. имеются две статически инвариантные величины: главный вектор системы сил и проекция главного момента на направление главного вектора.