Центр параллельных сил.

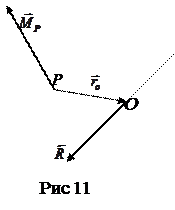Система параллельных сил, как было указано выше, приводится к равнодействующей. Докажем теорему Вариньона: если система сил приводится к равнодействующей, то момент этой равнодействующей, относительно произвольной точки равен геометрической сумме моментов сил относительно этой точки. Действительно, зависимость главного момента от центра приведения задаётся формулой (1.4)

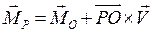
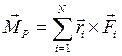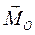Выберем точку О на линии действия равнодействующей. Тогда , но =0, как момент равнодействующей относительно точки, лежащей на линии её действия, и тогда

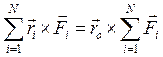(1.9)

Пусть для определённости все силы параллельны оси OZ , в этом случае можно записать 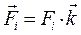, а формулу (1.9) переписать в виде

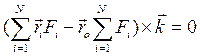(1.10)

Для выполнения условия (1.10) должно быть: или выражение в скобках равно нулю, либо выражение в скобках параллельно вектору 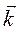, но мы выбрали направление OZ произвольно, следовательно, нулю должно быть равно выражение в скобках, из которого и получаем выражение для центра параллельных сил

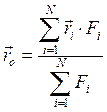(1.11)

Центр параллельных сил всегда находится на линии равнодействующей, но это особая точка. Если все силы повернуть на один и тот же угол, не меняя их точек приложения, то выражение в скобках формулы (12) и модуль равнодействующей не изменится, но сама равнодействующая повернётся на тот же угол вокруг центра параллельных сил. В проекциях на оси декартовой системы координат формула (1.11) записывается в виде

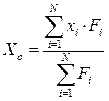
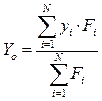
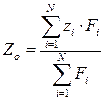(1.12)