Задача об опрокидывании тела. Трение качения.

Предположим, что рассматриваемое тело имеет вертикальную плоскость симметрии; пусть сечение тела этой плоскостью представляет прямоугольник со сторонами 2а и 2в (рис. 15).

К телу приложены вертикальная нагрузка (вес) Р и гори­зонтальная сила Q. 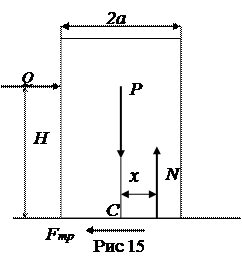Реакция плоскости основания на тело приводится к нормальной реакции N и силе трения Fтр, причем линия действия N неизвестна; ее расстояние от точки С обозначим через х. Оче­видно, х≤а. Составляем три уравнения равновесия плоской системы сил в виде двух уравне­ний проекций на горизонтальную и вертикальную оси и уравнения моментов относительно точки С:

N- P = 0, Q- Fтр=0, Nx-Q·H =0 (1.18)

Полученные три уравнения позволяют определить неизвестные реакции N, Fтр ,х. Согласно закону трения, при равновесии, имеем: F<fN. Перепишем уравнения (1.18) с учетом закона трения и условия х≤а.

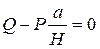, Q-Р·f=0,

Будем постепенно увеличивать Q. Если 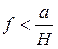, то равновесие будет иметь место до тех пор, пока сила трения не достигнет своей предельной величины, после чего начнется скольжение ползуна; если 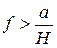, то тело раньше, чем начнется скольжение, опрокинется.

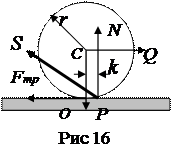Представим себе каток веса Р и радиуса r, покоящийся на гори­зонтальной плоскости (рис. 16). Опыт показывает, что, если прило­жить к оси катка горизонтальную силу Q, каток будет оставаться в покое, пока величина этой силы не достигнет некоторого значе­ния. Чтобы объяснить этот факт, составим уравнения статики для плоской системы сил, действующих на каток; этими силами являются вес P, усилие Q и реакция S, которую можно разложить на нормальную составляющую - реакцию N и горизонтальную - силу трения Fтр. Проектируя все силы на горизонтальное и вертикальное направ­ления, получим:

Q = Fтр, P = N.

Остается составить уравнение моментов; за центр моментов примем точку О, точку соприкосновения контура колеса с плоскостью; имеем:

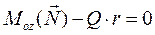
Мы приходим, таким образом, к необходимости принять, что нормальная реакция N приложена не в точке О, а несколько сдви­нута от нее в сторону действия силы Q. Физически этот сдвиг можно объяснить на­личием деформаций катка и опорной пло­скости в области точки О; фактически со­прикосновение происходит по некоторой пло­щадке, размеры которой зависят от величины нормального давления, свойств материалов и состояния поверхностей катка и опорной плоскости. Можно считать, что к катку приложена пара, момент которой равен 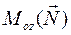, который называется моментом трения качения. Его предельная величина, как показывают опыты, пропорциональна нормальному давлению катка на плоскость: 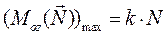, причем имеющий размерность длины коэффициент трения качения k определяется опытным путем. Очевидно, что k можно рассматривать как отрезок, на который сдвинута сила N в направлении силы Q в критический момент равновесия. Легко заметить, что задача трения качения практически полностью совпадает с задачей опрокидывания тела из предыдущего параграфа заменой 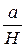на . 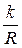Обычно 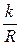- значительно меньше, чем f; это значит, что нарушение покоя, которое произой­дет при постепенном увеличении силы Q, будет заключаться в том, что каток начнет катиться по опорной плоскости, не скользя по ней. Возникающие здесь вопросы, однако, не могут быть рассмотрены без применения средств динамики.

Вопросы для самопроверки:

1. Что такое момент силы относительно точки?

2. Чему равен момент силы F с проекциями на оси декартовой системы координат (1,2,3) относительно оси Oy, если координаты точки ее приложения (0,1,5) (варианты Ox, Oz)?

3. Напишите условия равновесия сходящейся системы сил в векторной форме, а также в проекциях на оси декартовой системы координат.

4. Что такое пара сил, чему равен ее момент?

5. Как зависит главный момент от выбора центра приведения,

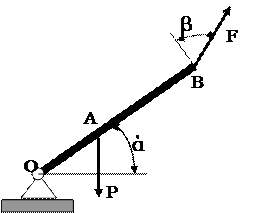
6. Чему равен момент силы Р=10 н и F=15н относительно оси 0Z , перпендикулярной плоскости рисунка, если ОА= 0.1м, АВ=0.15м Углы ά и β равны соответственно π/6 и π/4. Все силы лежат в плоскости чертежа.

Определите главный вектор заданных сил.

7. Какие уравнения равновесия необходимо записать для плоской системы сил, если все силы расположены в плоскости XOY ( варианты XOZ, YOZ )?

8. Крышка ABCD открыта на угол α=π/3 и удерживается в этом положении стержнем СЕ. Отношение АВ/ВС=3/4 Чему равны проекции силы F на указанные оси координат?

Чему равен момент силы F относительно оси OX (OZ)? АВ=L, сила F направлена по линии ВD.

9. Какие уравнения равновесия необходимо записать для системы сил, паралельных оси OY (варианты OX,OZ ) ?

10. Сформулируйте теорему Пуансо.

11. Какие статические инварианты Вам известны,?

12. В каких случаях система сил приводится к равнодействующей?

13. Приведите указанную на рисунке систему сил к прстейшему виду. Равные силы направлены по диагоналям граней кубика со стороной b.

14. В каких случаях момент силы относительно оси равен нулю ?

15. Сформулируйте теорему Вариньона.

16. Векторная формула центра параллельных сил.

17. Докажите, что система параллельных сил приводится к равнодействующей.

18. Векторная формула центра тяжести, прокомментируйте введенные обозначения.

19. Где находится центр тяжести указанной фигуры, состоящей из квадрата и равностороннего треугольника со стороной в?

20. Чему равна сила трения в указанном примере, если вес груза 100 н, угол наклона плоскости π/4, сила F=50н, а коэффициент трения скольжения f=0.4?

РАЗДЕЛ ВТОРОЙ

КИНЕМАТИКА

__________________________________________________________

В разделе кинематики мы изучаем движение и устанавливаем основные пространственно – временные характеристики движения. В настоящем разделе, посвященном кинематике, отвлекаются от силовых взаимодействий между материальными телами и влияния на них силовых полей, а рассматривают механические движения тел, в отрыве от причин, которые создают и поддерживают эти движения. Движения в кинематике изучаются по отношению к некоторой системе отсчёта, представляющей жесткую, неограниченно простирающуюся во все стороны систему точек. В кинематике неважно, движется ли эта система или принимается неподвижной. Отметим, что такое равноправие систем не имеет места в динамике. В этом пространстве выбирается тело отсчёта, а в нём систему координат, например, три взаимно перпендикулярные координатные оси, служащие для определения положения отдельных точек тел.

Как указывалось в начале, пространство рассматривается как евклидово, так, применение теоремы Пифагора позволяет определить квадрат расстояния между двумя точками как сумму квадратов разностей соответствующих координат точек и т. п. Наряду с абсолютным пространством в классической кинематике используется понятие «абсолютного времени», одинаково и равномерно текущего во всех точках абсолютного пространства. В качестве такого времени принимается звёздное или среднее солнечное время. Заметим, что все выводы классической механики с достаточной для практики точностью справедливы, если скорости движения малы по сравнению со скоростью распространения света, а размеры областей пространства, в которых происходит движение, далеки от космических расстояний.

Глава 4.

Кинематика точки.