Трение скольжения Угол трения, конус трения.

Явления трения скольжения впервые экспериментально изучались в конце XVII в. французским физиком Амонтоном (1663—1705), законы трения были сформулированы почти сто лет спустя Кулоном (1736-—1806).

1. Сила трения лежит в плоскости касательной к соприкасающимся поверхностям трущихся тел.

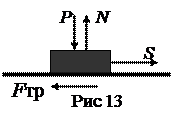2. Сила трения не зависит от площади соприкосновения тел.

3. Максимальное значение силы трения пропорционально нормальному давлению N тела на плоскость (в рассматриваемом случае N=P):

F max= fN

К телу веса P, лежащему на горизонтальном столе (рис.13), будем прикладывать горизонтальное усилие S. Размерами тела пренебрегаем, рассматривая его как материальную точку (случай тела конечных размеров рассмотрен ниже). Если S =0, тело будет в равновесии (в данном случае в покое по отношению к столу); если силу S начнем увеличивать, то тело все же будет оставаться в покое; следовательно, горизонтальная состав­ляющая реакции стола, называемая силой трения Fтр уравновешивает приложенную силу S и воз­растает вместе с нею до тех пор, пока равно­весие не нарушится. Это произойдет в тот момент, когда сила трения достигнет своего максимального значения.

F max= fN (1.17)

причем коэффициент пропорциональности f, называемый коэффици­ентом трения скольжения, определяется экспериментально и ока­зывается зависящим от материала и состояния (шерохова­тости) поверхностей трущихся тел. Численное зна­чение коэффициента трения скольже­ния для различных материалов можно найти в справочниках. Наряду с коэффициентом трения f введем в рассмотрение угол трения φ, определяя его соотношением 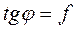. Происхождение этого равенства и наименование «угол трения» будут объяснены ниже. Когда Р достигнет значения Fmах, наступит критический (пуско­вой) момент равновесия; если S останется равным Fmax, то равновесие не нарушится, но достаточно самого ничтожного приращения усилия S, чтобы тело сдвинулось с места. Можно заметить, что как только тело сдвинется с места, сила трения сразу несколько умень­шится; опыты показали, что трение при взаимном движении тел не­сколько меньше трения при взаимном покое их. Важно отметить, что до наступления критического момента, т. е. пока тело находится в покое, сила трения равна приложенному усилию и можно лишь утверждать, что F≤ 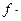N. Знак равенства относится к критическому моменту равновесия. Направление силы трения при покое противоположно направле­нию силы S и меняется с изменением направления этой силы.

Коэффициент трения f зависит от скорости тела, уменьшаясь для большинства материалов при увели­чении скорости. ( Как на исключение, можно указать на случай трения кожи о металл; здесь f увеличивается при увеличении относительной скорости.). Соотношение (17) достаточно хорошо отвечает наблюдениям при трении сухих или слабо смазанных тел; теория трения при наличии слоя смазки, созданная Н. П. Петровым и О. Рейнольдсом, представляет специальный раздел гидродинамики вязкой жидкости.

Угол трения, конус трения.

Рассматривая трение покоя, предположим, что к телу, покоящемуся на горизонтальной шерохо­ватой плоскости, приложена сила Q, составляющая угол α с нор­малью к плоскости (рис. 14). Составим уравнения равновесия. Для сходящейся системы сил достаточно написать два уравнения

.

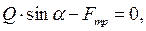
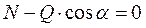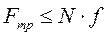Написанные уравнения определяют силу трения и нормальную реакцию. Для того чтобы тело под действием приложенного усилия не могло быть сдвинуто с места, необходимо, чтобы или 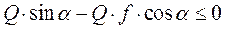. Разделив полученное неравенство на 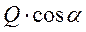, имеем 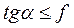, или вводя угол трения, получаем α ≤φ. Следовательно, в зависимости от материала и характера поверх­ности трущихся тел можно по заданному коэффициенту трения определить такой угол φ , что если приложенная к телу сила будет наклонена к нормали на угол, меньший угла φ, то как бы ни была велика эта сила, тело останется в равновесии. Это и объясняет наименование угла φ углом трения. Область внутри отрезков с углом 2φ («область трения») представляет область, обладающую замечатель­ным свойством: как бы ни была велика по интенсивности сила, линия действия которой расположена внутри этой области, эта сила не приведет в движение тело, опирающееся на плоскость.

Если мы рассматриваем тело, имеющее возможность передвигаться в любом направлении вдоль плоскости, то область трения будет ограничена поверхностью конуса с углом растворения, рав­ным 2φ (так называемым конусом трения). Наличием области трения объясняется явление заклинивания или, как говорят, «заедания» частей машин, когда никакой силой, приложенной внутри конуса, не удаётся сдвинуть соответствующую часть машины. Коэффициент трения может иметь различные значения для различных направлений на плоскости (например, при трении по дереву вдоль и поперек волокон, при трении по прокатному железу по направлению и перпендику­лярно к направлению прокатки). Поэтому конус трения не всегда представ­ляет прямой круглый конус.